
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Відкриті множини метричних просторів та їх властивості
Нехай  - метричний простір,
- метричний простір,  - елемент простору,
- елемент простору,  .
.
Множина  називається відкритою кулею з центром у точці
називається відкритою кулею з центром у точці  і радіусом
і радіусом 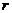 .
.
Множина  називається замкненою кулею з центром у точці
називається замкненою кулею з центром у точці  і радіусом
і радіусом 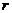 .
.
Множина  називається сферою з центром
називається сферою з центром  і радіусом
і радіусом 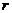 .
.
Множину  називають
називають  -околом точки
-околом точки  .
.
В метричному просторі можна ввести означення відстані між його підмножинами,а саме, якщо  , то
, то 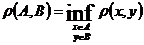 .
.
Означення відстані між підмножинами дозволяє ввести означення  -околу підмножини А метричного простору. А саме, якщо
-околу підмножини А метричного простору. А саме, якщо 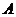 міститься в М, то
міститься в М, то

Нехай М - метричний простір, U – підпростір простору М, називають відкритою множиною, якщо або U – пуста множина, або будь-яка точка з U входить в U разом з деяким своїм  -околом. Тобто
-околом. Тобто

Твердження 1: Нехай М – метричний простір,  , тоді:
, тоді:
- Відкрита куля
 - відкрита множина.
- відкрита множина. -
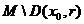 - відкрита множина.
- відкрита множина.
Доведення: Нехай  .
.
Покажемо, що 
Нехай 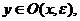 тоді
тоді

Таким чином,  .
.
Оскільки 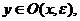 то весь цей окіл належить
то весь цей окіл належить 


1 пункт доведено.
Нехай 
Нехай 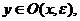 тоді за аксіомою трикутника, маємо:
тоді за аксіомою трикутника, маємо:

Таким чином, 
Оскільки 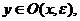 то весь цей окіл належить
то весь цей окіл належить 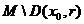

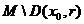
Все доведено.
Теорема 2 (властивості відкритих множин метричного простору):
Нехай М – метричний простір, тоді сукупність усіх відкритих множин простору М задовольняє наступним властивостям:
- Пуста підмножина та вся множина М є відкритими.
- Об’єднання будь-якої кількості відкритих підмножин простору М є множиною відкритою.
- Перетин будь-якої скінченної сукупності відкритих підмножин з М – відкрита множина в М.
Доведення: 1. За означенням відкритої множини пуста множина є відкритою, а будь-яка точка з М входить у простір М з будь-яким своїм околом. Тому М – також відкрита.
- Нехай
 - деяка сукупність відкритих множин простору М
- деяка сукупність відкритих множин простору М

Покажемо, що U – відкрита множина М.
Нехай 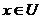 , тоді
, тоді 
Оскільки 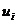 - відкрита, то
- відкрита, то 
Але за означенням об’єднання: 
Таким чином, 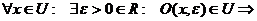 U – відкрита.
U – відкрита.
- Нехай
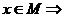 за означенням перетину:
за означенням перетину:

Оскільки підмножини 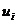 - відкриті, то
- відкриті, то  . Нехай
. Нехай
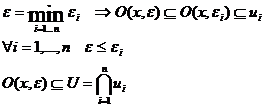
Таким чином, кожна точка U входить в U разом з деяким своїм околом  U – відкрита підмножина.
U – відкрита підмножина.
Зауваження: Перетин нескінченної сукупності відкритих підмножин метричного простору може бути відкритим.
Розглянемо відкриті підмножини:
 не є відкритою підмножиною, оскільки ніякий окіл числа 1 не попадає в множину (0,1].
не є відкритою підмножиною, оскільки ніякий окіл числа 1 не попадає в множину (0,1].
Твердження 2: Підмножина U множини М є відкритою тоді і тільки тоді, коли U є об’єднанням деякої сукупності відкритих куль з М.
Доведення: Нехай U є об’єднанням деякої сукупності відкритих куль. За твердженням 1 кожна ця куля є відкритою підмножиною, тоді за властивістю 2 попередньої теореми: U – також відкрита підмножина з М.
Нехай U – відкрита підмножина з М, тоді за означенням відкритої підмножини:

Оскільки 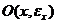 - відкриті кулі, то твердження доведено.
- відкриті кулі, то твердження доведено.
Не нашли, что искали? Воспользуйтесь поиском: