База топологічного простору. Введення топології за допомогою бази

Нехай - топологічний простір, - його топологія. називається базою топології , якщо будь-яка підмножина з є об’єднанням деякої сукупності підмножин з (при цьому вважається, що є об’єднанням пустої сукупності підмножин з ).

Твердження 1 (критерій бази): - топологічний простір. є базою топології тоді і тільки тоді, коли

Доведення: Припустимо, що - база топології . Виберемо довільну точку і деякий її окіл . Оскільки є відкритою множиною, то він є об’єднанням деякої сукупності підмножин . Оскільки , то з означення об’єднання випливає, що .

Припустимо тепер, що задовольняє умові критерію, і покажемо, що тоді - база топології , тобто будь-яка відкрита підмножина є об’єднанням деякої сукупності підмножин з .

Дійсно, оскільки 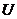- відкрита, то . Тоді за умовою критерію:

. Все доведено.

Приклади: 1. З розділу “Відкриті підмножини метричного простору ” випливає, що утворює базу індукованої топології . Оскільки будь-яка відкрита підмножина з М є об’єднанням деякою сукупності відкритих куль. Але ця топологія має і меншу базу: .

1. В природній топології числової прямої R базу утворюють усі обмежені відкриті інтервали . Відзначимо, що хоча ця топологія на R має потужність контінум, але вона має зліченну базу , що випливає з критерію бази.

Твердження 2 (необхідна умова бази): Нехай - топологічний простір. Якщо є базою топології , то задовольняє наступним умовам:

1.

2.

Доведення: 1. Оскільки Т – відкрита множина, то Т можна представити як об’єднання елементів бази . За означенням об’єднання .

1. Нехай - відкрита множина, як перетин двох відкритих множин.

- окіл точки х і за критерієм бази . Все доведено.

Теорема(про введення топології за допомогою бази): Нехай Т – деяка множина і . Припустимо, що задовольняє умовам 1) і 2) попереднього твердження, тоді існує єдина топологія на Т, для якої є базою.

Доведення: Нехай - сукупність усіх можливих об’єднань підмножин з . Перевіримо аксіоми топології для :

Т1: З умови 1) попереднього твердження випливає, що Т є об’єднання деякої сукупності підмножин з . Таким чином, .

Пусту множину можна розглядати як об’єднання пустої сукупності підмножин з , тому .

Т2 – виконується, оскільки об’єднання будь-якої сукупності об’єднань підмножин з буде об’єднанням підмножин з , тому потрапляє в .

Т3: Для доведення цієї аксіоми застосуємо метод математичної індукції:

а) Нехай .

Покажемо, що .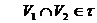

Дійсно, .

Достатньо показати, що , тоді з аксіоми Т2 випливає, що .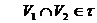

Згідно умові 2) попереднього твердження:

Тоді цей перетин є

б) Припустимо, що перетин будь-якої k підмножин з належить . Покажемо, що перетин k+1 підмножин з також належить :

. Все доведено.

Не нашли, что искали? Воспользуйтесь поиском: