Точки дотику. Замикання підмножин топологічного простору

Нехай Т – топологічний простір, називається точкою дотику до підмножини А, якщо .

Сукупність усіх точок дотику А називається замиканням підмножини А. ([А])

Теорема (властивості операції замикання):

Нехай Т – топологічний простір, тоді операція замикання в Т має такі властивості:

1.

2.

3.

4.

Доведення: 1)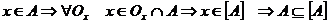

2)

3)

Покажемо, що

Можна розглядати як окіл у, а оскільки ує[А], то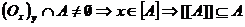

4)

Покажемо, що

Застосуємо метод математичної індукції:

Базис

Індуктивне припущення:

Індуктивний перехід: .

Все доведено.

Нехай Т – топологічний простір, - замкнена тоді і тільки тоді, коли

.

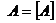Доведення: Припустимо, що А – замкнена, тоді - відкрита, тобто

х не є точкою дотику.

Отже, не містить точок дотику, тому вони попадають в А. Але .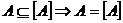

Припустимо тепер, що 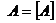, слідовно всі точки дотику містяться в А, тому не має точок дотику - відкрита, тому А – замкнена. Все доведено.

Твердження: Нехай Т – топологічний простір, Тоді 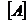- перетин усіх замкнених підмножин з Т, що містять А.

Доведення: Нехай F – перетин усіх замкнених підмножин з Т, що містять А.

Тоді F – замкнена підмножина, яка містить А.

Покажемо, що . Дійсно, оскільки відкрита, то

х не є точкою дотику до А, тому усі точки дотику містяться в F.

Оскільки , то 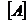- замкнена .

Не нашли, что искали? Воспользуйтесь поиском: