Топологія. Топологічні простори. Приклади

Нехай Т – деяка множина, тоді булеан - сукупність усіх підмножин.

Деяка сукупність підмножин множини називається топологією на множині Т, якщо задовольняє наступним аксіомам (аксіомам топології)

Т1: пуста множина, сама множина Т містяться в .

Т2:

Об’єднання будь-якої сукупності підмножин з також належить до .

Т3:

Перетин скінченної сукупності підмножин з належить до .

Якщо на множині Т задана деяка топологія , то пару (Т, ) називають топологічним простором. При цьому елементи множини Т називаються точками цього простору. А підмножини з називаються відкритими підмножинами з цього простору.

Якщо заздалегідь невідомо, про яку топологію на Т йде мова, то для позначення топологічного простору можна використовувати лише позначення множини Т.

Приклад 1: (М, 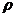) – деякий метричний простір.

Нехай - сукупність всіх відкритих підмножин цього простору. За теоремою задовольняє всім аксіомам топології, тоді (М, ) є топологічним простором. Цю топологію називають топологією на М, індукованою метрикою 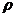, і позначається .

Таким чином, поняття топологічного простору є деяким узагальненням метричного простору.

Нехай (Т, ) – деякий топологічний простір. Якщо на множині Т можна задати метрику 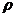, так що 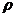(Т, )=(Т, ), то кажуть, що топологія є метризованою.

Зазначимо, що далеко не всі топології є метризованими.

Приклад 2: Нехай Т – множина. = , тоді - топологія на Т, яку називають дискретною. Зазначимо, що дискретна топологія індукована дискретною метрикою. У цій топології усі підмножини з Т є відкритими. І зокрема, точки дискретного простору є відкритими підмножинами.

Приклад 3: Нехай Т – множина. , задовольняє всім аксіомам топології. Цю топологію називають тривіальною топологією на Т.

Приклад 4: Нехай Т – нескінченна множина, покладемо:

є топологією на Т, яку називають топологією скінченних доповнень (топологією Заріського). Перевіримо, що є топологією на Т:

З означення випливає Т1

Т2: Нехай

Розглянемо кількість

Якщо усі 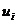- пусті підмножини, то .

Якщо не всі – то їх можна не писати в об’єднання.

Таким чином, можна вважати, що всі множини 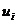є не пусті.

Т3:

Якщо хоча б одна з множин 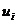пуста, то 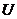також пуста з .

Приклад 5: Нехай (Т, ) – топологічний простір і нехай

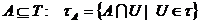
Покажемо, що 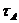є топологією на множині А.

Т1:

Т2:

Т3: Нехай

Таким чином, 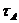- топологія на підмножині А, яку називають топологією, індукованою на А топологією називають підгрупою простору .

Таким чином, всяку підмножину простору Т можна розглядати як його підпростір з індукованою топологією.

Якщо , то - слабкіша, 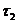- сильніша. Найслабкіша – тривіальна , найсильніша – дискретна

Не нашли, что искали? Воспользуйтесь поиском: