Ізольовані, граничні, межові точки

Нехай Т – топологічний простір, Тоді

Точка К, яка належить множині А, називається ізольованою точкою множини А, якщо

Множина усіх ізольованих точок з А позначається IsA.

Точка х, яка належить множині Т, називається граничною, якщо

. Множина усіх граничних точок А позначається і називається похідною множини А.

Точка х, яка належить множині Т, називається межовою точкою множини А, якщо . Сукупність межових точок – це межа А (FrA).

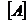Твердження 1: Нехай Тоді розпадається на три множини, що не перетинаються:

1. IsA.
2. - граничні точки А, що належать А.
3. - граничні точки А, що не належать А.

Доведення: З означення граничної точки та точок дотику випливає, що будь-яка гранична точка є точкою дотику: .

А розглянувши ще означення ізольованих точок, бачимо, що будь-яка точка дотику є або граничною точкою, або ізольованою:

Оскільки означення ізольованих і граничних точок є несумісними, то перетин – пуста множина: .

Множина розпадається в об’єднання двох підмножин, що не перетинаються: . Все доведено.

Наслідок 1: Підмножина А множини Т є замкненою тоді і тільки тоді, коли вона містить усі свої граничні точки.

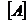Твердження 2: Нехай Тоді розпадається в об’єднання трьох підмножин, що не перетинаються:

Доведення: З означення межових точок та точок дотику випливає, що всяка межова точка є точкою дотику, тобто . Розглянувши ще означення внутрішніх точок, бачимо, що будь-яка точка дотику є або межовою, або внутрішньою точкою (якщо ).

Таким чином, .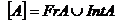

Оскільки означення межових та внутрішніх точок є несумісними, то .

У свою чергу, розпадається в об’єднання двох підмножин, що не перетинаються: . Все доведено.

Наслідок 2: є замкненою тоді і тільки тоді, коли вона містить усі свої межові точки.

Наслідок 3: Тоді:

1.

2.

3.

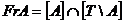
Приклади: 1.

2.

Не нашли, что искали? Воспользуйтесь поиском: