Непрерывные случайные величины. Интегральная функция распределения непрерывной случайной величины. Основные свойства функции распределения. Интегральная кривая распределения.

Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны.

Функция распределения случайной величины (интегральная функция распределения вероятностей) - это функция, определяющая для каждого значения x вероятность того, что случайная величина (ξ) примет значение меньшее, чем x: F(x) = P(ξ < x). Численно функция распределения (интегральная кривая распределения) равна площади фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом.

Основные свойства функции распределения:

1°. Функция распределения является неубывающей.

2°. Значения функции распределения удовлетворяют неравенствам .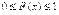

3°. Вероятность того, что дискретная случайная величина ξ примет одно из возможных значений x_i, равна скачку функции распределения в точке x_i.

Определение и основные функции дифференциальной функции распределения (плотности распределения) для непрерывной случайной величины. Кривая плотности распределения. Равномерное распределение непрерывной случайной величины.

Предел отношения вероятности попадания непрерывной случайной величины в интервал от х до х+∆х к длине этого интервала ∆х, когда ∆х стремится к нулю, называется дифференциальной функцией распределения вероятностей (плотностью распределения) случайной величины в точке х и обозначается f(х).

Смысл плотности распределения f(х) состоит в том, что она указывает на то, как часто появляется случайная величина Х в некоторой окрестности точки x при повторении опытов.

Кривая, изображающая плотность распределения f(х) случайной величины, называется кривой распределения.

Случайная величина Х называется непрерывной, если её интегральная функция распределения F(х) непрерывна на всей числовой оси 0х, а плотность распределения f(х) существует везде, за исключением конечного числа точек.

Свойства функции плотности распределения вероятностей:

Свойство 1. Плотность распределения неотрицательна, т.е. f(х)≥0.

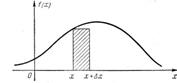
Свойство 2. Интегральная функция распределения случайной величины равна интегралу от плотности вероятности в интервале от - ∞ до х (заштрихованная область на рисунке).

Свойство 3. Вероятность попадания непрерывной случайной величины Х в интервал равна определенному интегралу.

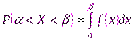
Свойство 4. Интеграл по всей числовой оси от плотности вероятности равен единице.

Непрерывная случайная величина имеет равномерное распределение на отрезке [a;b], если на этом отрезке плотность распределения данной случайной величины постоянна, а вне его равна нулю.

График плотности для равномерного распределения

Непрерывная случайная величина подчиняется закону равномерного распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все значения случайной величины одинаково вероятны.

21.Числовые характеристики случайной величины. Математическое ожидание: определение и основные свойства. Вычисление математического ожидания для дискретной и непрерывной случайных величин. Вероятностный смысл математического ожидания.

Числа, которые описывают случайную величину суммарно, называют числовыми характеристиками случайной величины: дисперсия, мода и медиана, моменты случайных величин, математическое ожидание.

Математическое ожидание случайной величины - среднее взвешенное значение случайной величины.

(для дискретной величины)

где – возможные значения случайной величины Х, а – соответствующие вероятности.

(для непрерывной величины)

Вероятностный смысл математического ожидания: математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Свойства математического ожидания:

1. Математическое ожидание постоянной равно самой этой постоянной.

2. Математическое ожидание алгебраической суммы случайных величин равно алгебраической суме их математических ожиданий.

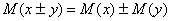
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

М(xy) = M(x) * M(y)

22. Дисперсия случайной величины: определение и основные свойства. Вычисление дисперсии для дискретной и непрерывной случайных величин. Среднее квадратическое отклонение случайной величины.

Дисперсия случайной величины — мера разброса данной случайной величины, её отклонения от математического ожидания.

Для дискретной случайной величины Х дисперсия вычисляется по формуле

Для непрерывной:

Дисперсия обладает следующими свойствами:

1. Дисперсия постоянной равна нулю:

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:

D(CX) = C²*D(X)

3. Дисперсия суммы (разности) независимых случайных величин равна сумме (разности) дисперсий слагаемых:

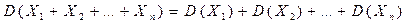
4. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появ­ления и не появления события в одном испытании:

D(X) = npq

Среднее квадратичное отклонение – корень квадратный из дисперсии. Ее обозначают греческой буквой «сигма»

Не нашли, что искали? Воспользуйтесь поиском: