Закон больших чисел. Теорема Чебышева. Центральная предельная теорема. Теорема Ляпунова.

Под законом больших понимается ряд теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.

Теорема Чебышева. Пусть имеется бесконечная последовательность x₁,x₂,.. независимых случайных величин с одним и тем же математическим ожиданием m и дисперсиями, ограниченными одной и той же постоянной:

M[x₁] = M[x₂] = … = m

D[x₁] < c, D[x₂] < c,…

Тогда каково бы ни было положительное число e, вероятность события |((x1+…+xn)\n)-m|<e, стремится к 1 при n стремящемся к бесконечности.

Центральная предельная теорема: Если Х₁, Х₂,…, Х_n - независимые случайные величины с одинаковым законом распределения, математическим ожиданием и дисперсией, то при неограниченном увеличении n закон распределения суммы неограниченно приближается к нормальному.

Теорема Ляпунова: Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, для которых выполнено условие:

где b_k – третий абсолютный центральный момент величины Х_к, а D_k – ее дисперсия, то Х имеет распределение, близкое к нормальному.

Основные понятия математической статистики (генеральная совокупность и выборка, вариационный ряд, варианта, частота). Эмпирическая функция распределения.

Основной целью математической статистики является установление закономерностей, которым подчиняются массовые случайные явления. Для этого решаются следующие основные задачи: определение способов сбора и обработки информации — результатов наблюдений.

Выборочной совокупностью (выборкой) называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность всех объектов, из которых производится выборка.

Например: Выборкой является совокупность чисел -2, -1, 3, 5, 10. А генеральной совокупностью положительных чисел будет являться 3, 5, 10.

Вариационный ряд – ряд, в котором сопоставлены (по степени возрастания или убывания) варианты и соответствующие им частоты

​Варианты – отдельные количественные выражения признака. Обозначаются V.

Частота – число, показывающее, сколько раз повторяется варианта. Обозначается P. Сумма всех частот (которая, разумеется, равна числу всех исследуемых) обозначается как n. Например, в вариационном ряду показателей систолического артериального давления, измеренного у десяти пациентов: 110, 120, 120, 130, 130, 130, 140, 140, 160, 170. Вариантами являются только 6 значений: 110, 120, 130, 140, 160, 170. ​Для варианты 110 частота Р = 1 (значение 110 встречается у одного пациента).

Эмпирической функцией распределения (или функцией распределения выборки) называют функцию , где n_x — число вариант со значением меньше x.

Точечные оценки параметров распределения. Требования к оценкам. Выборочная средняя как оценка математического ожидания теоретического распределения. Генеральная и выборочная дисперсия. Исправленная дисперсия.

Оценивание параметров распределения осуществляется в два этапа. На первом этапе, на основании выборки х₁, х₂,...,,х_n,строится статистика,

,

значение которой принимают за приближенное значение оцениваемого параметра.

Так как параметр генеральной совокупности оценивается числом, которое на числовой оси изображается точкой, то оценку называют точечной.

Второй этап оценивания состоит в выборе наилучшей оценки, что требует введения критерия качества получаемых оценок.

Для того чтобы оценка имела практическую ценность она должна обладать следующими свойствами.

1. Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности:

2. Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности:

3. Эффективность оценки. Нужно выбрать такую оценку, у которой дисперсия была бы минимальной:

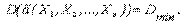
Такая оценка называется эффективной.

Выборочной средней называется среднее арифметическое значение количественного признака выборочной совокупности:

х`= (х1, х2, …, хn)/n

Поскольку, х₁, х₂, …, х_n –значения величин Х₁, Х₂,..,Х_n c одинаковым математическим ожиданием (МО) М_xi =а и дисперсией D_xi=σ₂,то МО и дисперсия среднего значения будут равны М (Х`) = a и D (X`) = σ₂/n.

Значит, среднее значение является несмещённой оценкой математического ожидания. Оценка состоятельна поэтому, что если по нескольким выборкам большого объема из одной генеральной совокупности будут выбраны средние, то они будут мало отличаться друг от друга (свойство устойчивости выборочных средних).

Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения.

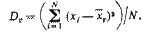
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию. Для исправления выборочной дисперсии достаточно умножить ее на дробь:

28.Интервальные оценки параметров распределения. Доверительная вероятность (надежность). Доверительный интервал. Доверительные интервалы для оценки математического ожидания нормального распределения при известном «сигма» и при неизвестном «сигма».

Интервальной называют оценку, которая определяется двумя числами – концами интервала.

Надежность выполнения неравенства оценивается числом g (α = 1 – γ), которое называют доверительной вероятностью:

g = Р()

где, число ε характеризует точность оценки параметра θ; число g – характеризует надежность оценки параметра θ.

Очевидно, чем больше требуется точность ε (т. е., чем меньше длина доверительного интервала), тем меньше вероятность накрыть интервалом искомый параметр θ, и, наоборот, с уменьшением точности ε (увеличением длины доверительного интервала) увеличивается надежность g накрыть интервалом параметр θ.

Интервальная оценка математического ожидания при известной дисперсии

Интервальная оценка математического ожидания при неизвестной дисперсии.

Не нашли, что искали? Воспользуйтесь поиском: