Проверка статистической гипотезы о соответствии фактического выборочного распределения распределению Пуассона

Условие: Имеется эмпирический ряд распределения тракторов по числу поломок (таб. 2.5).

Проверить нулевую гипотезу о соответствии эмпирического распределения распределению Пуассона. Уровень вероятности суждения 0,95.

Решение:

1. Выдвинем нулевую и альтернативную гипотезу:

Н_о: эмпирическое распределение соответствует распределению Пуассона,

Н_а: эмпирическое распределение не соответствует распределению Пуассона.

2. Исходя из предположения о соответствии эмпирического распределения теоретическому определим гипотетические частоты. С этой целью:

а) определим произведение значений признака на частоту встречаемости (x_i n_i) и сумму произведений (итог графы 3)

б) рассчитаем среднее значение признака совокупности по средней арифметической взвешенной =

в) Рассчитаем дисперсию признака, используя итог графы 5 и квадрат средней арифметической

=

г) гипотетические частоты для возможных значений признака определяем, используя функцию

Р _{(х= m)} =

где λ – параметр распределения Пуассона (за его приближенную оценку принимаются значения 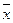и S², в рассматриваемом примере λ ≈ 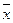≈ S² ≈ 0,60)

- постоянная величина, основание натурального логарифма

m – возможные значения признака, соответствующие х _I

Определим λ^m и запишем значения в графу 6.

Для значения х₁ λ^m = 0,60⁰ = 1.0000

Для значения х₂ λ^m = 0,60¹ = 0,6000 и т.д.

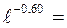д) по таблице значений (приложение 7) найдем = = 0,5488 и определим произведение (графа 7)

ж) определим вероятность существования каждого значения признака по формуле Р _{(х= m)} = и проверим равенство Σ р_i =1.000 (графа 9)

з) рассчитаем гипотетические частоты распределения Пуассона по формуле ň_I=Np_i, найдем сумму теоретических частот и проверим ее равенство фактических частот Σn_{i =} Σ ň _i = N = 2650.(графа 10)

е) определим (графа 8)

3. Определим разности фактических и гипотетических частот и проверим равенство их сумм нулю. Σ(n_i -ň _i)=0 (графа 11)

4. Найдем квадраты разностей частот (графа 12)

5. Рассчитаем фактическое значение критерия χ² по формуле χ² _факт = = 6,8859

6. Определим число степеней свободы вариации по формуле V= L - k – m,

где L- число интервалов (градаций признака), k –число независимых линейных ограничивающих связей, m – число параметров, использованных при исчислении гипотетических частот.

В рассматриваемом примере число градаций признака равно 5, ограничивающих линейных связей – 1 (Σn_{i =} Σ ň _i = N), при исчислении гипотетических частот использован 1 параметр - λ.

V=5-1-1=3

7. По таблице «Критические значения критерия χ²» (Приложение 6), найдем критическое значение χ² при α= 0,05, V =3

χ²_таб. = 7,81

8. Сопоставим фактическое и табличное значение χ².

Таблица - 2.5 Эмпирическое и теоретическое распределение тракторов по числу поломок

Число поломок (значение признака)	Число тракторов (частота)	Объем явления	Квадрат значения признака	Произведение квадрата значения на частоту	λm			Р (х= m) =	Гипотетическая частота	Разность	Взвешенный квадрат разности
xi	ni	xi ni	xi2	xi2 ni	ňi= piN	ni -ň i	(n i - ň i)2 ň i
					1,0000	0,5488		0,5488		-4	0,0110
					0,6000	0,3294		0,3294		-13	0,1938
					0,3600	0,1976		0,0988		+28	2,9924
					0,2160	0,1200		0,0200		-13	3,1887
					0,1296	0,0711		0,0030		+2	0,5000
Итого			х		х	х	х	1,0000			6,8859

Фактическое значение критерия 6,8859 меньше его критического значения 7,81, следовательно, находится в области допустимых значений критерия. Следует принять нулевую гипотезу о соответствии фактического распределения распределению Пуассона с вероятностью ошибки 5 случаев из 100. Практически значимый вывод: фактические численности распределяются по закону Пуассона с вероятностью ошибки 5%.

Не нашли, что искали? Воспользуйтесь поиском: