Задача 2.5 Проверка статистических гипотез относительно двух средних величин по данным малых выборок

2.5.1 Выборки независимые с равными численностями (п ₁= п ₂), дисперсии генеральных совокупностей равны ()

Условие. Имеются выборочные данные о среднесуточных приростах поросят при разных типах кормления (табл.2.10).

Проверить статистическую гипотезу относительно средних генеральных совокупностей. Уровень значимости 0,05.

Таблица - 2.10 Среднесуточные приросты поросят при разных типах кормления

Тип кормления №1	Тип кормления № 2
единица выборки	среднесуточный прирост, г	отклонение от среднего прироста	квадрат отклонения	единица выборки	среднесуточный прирост, г	отклонение от среднего прироста	квадрат отклонения
	x 1 i				x 2 i
		+28				-4
		+8				-34
		+38				+36
		-42				+16
		-32				-14
Итого		-		Итого		-

Решение.

1. Сформулируем нулевую и альтернативную гипотезы:

Н₀: Среднесуточный прирост поросят при разных типах кормления в генеральной совокупности одинаков

Н_А: Среднесуточный прирост поросят при разных типах кормления в генеральной совокупности различен

2. Рассчитаем средние величины по выборкам:

(г); (г)

3. Вычислим выборочные дисперсии:

;

5. Определим обобщенную среднюю ошибку двух выборочных средних:

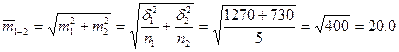(г)

6. Рассчитаем фактическое значение критерия t:

t_факт. =

7. Табличное значение критерия определим с учетом формирования независимой выборки. Численности выборок равны. Выясним, равны ли дисперсии в генеральных совокупностях. С этой целью проведем проверку гипотез по критерию F- распределения.

Н₀ : ; (в генеральных совокупностях дисперсии равны); Н_А: .

F_факт.= где s₁²>s₂² ; F_факт.= ;

F _{при и числе степеней свободы 4 и 4}= 6,39;

Фактическое значение критерия меньше табличного, следовательно .

8. Найдем по таблице критических значений двухстороннего критерия

t - Стьюдента (приложение 2) значение t при уровне значимости 0,05 и числе степеней свободы v = 2n-2=10-2=8: t_0,05=2,306

9. Сделаем статистически значимый вывод: Поскольку t_факт.> t_0,05, нулевую гипотезу о равенстве средних в генеральных совокупностях отвергаем. Следовательно, принимаем альтернативную гипотезу о том, что средние в генеральных совокупностях не равны с вероятностью ошибки 5%.

Практически значимый вывод: среднесуточный прирост поросят существенно зависит от типа кормления. Вероятность ошибки суждения- 5%.

2.5.2. Выборки независимые с разной численностью (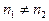), дисперсии генеральных совокупностей равны ()

Условие. Имеются выборочные данные об урожайности смородины по двум сортам (табл.2.11.).

Проверить статистическую гипотезу относительно средних величин генеральных совокупностей. Уровень значимости 0,05.

Таблица -2.11 Урожайность смородины по двум выборочным совокупностям.

Выборка 1 (сорт 1)	Выборка 2 (сорт2)
единица выборки	урожай-ность, кг с куста	отклонение от средней урожайности	квадрат отклоне-ния	единица выборки	урожай-ность, кг с куста	отклонение от средней урожай-ности	квадрат отклонения
	x 1 i				x 2 i
	5,6	+0,1	0,01		3,1	-0,6	0,36
	5,8	+0,3	0,09		3,6	-0,1	0,01
	4,9	-0,6	0,36		4,4	+0,7	0,49
	5,1	-0,4	0,16		-	-	-
	6,1	+0,6	0,36		-	-	-
Итого	27,5	-	0,98	Итого	11,1	-	0,85

Решение.

1. Сформулируем нулевую и альтернативную гипотезы:

Н₀: Средняя урожайность 1 сорта в генеральной совокупности равна средней урожайности 2 сорта.

Н_А: Урожайности по сортам различны.

2. Исчислим средние величины по выборкам:

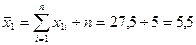(кг); (кг)

3. Вычислим выборочные дисперсии:

;

4.Определим обобщенную среднюю ошибку двух выборочных средних:

4. Рассчитаем фактическое значение критерия t:

t_факт. =

5. Табличное значение критерия определим с учетом формирования независимой выборки. Численности выборок не равны. Выясним, равны ли дисперсии в генеральных совокупностях. С этой целью проведем проверку гипотез по критерию F- распределения.

Н₀ : ; Н_А: .

F_факт.= где s₁²>s₂² . s² для 1–й выборки =

s² для 1–й выборки =

F_факт.= ;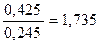

F _{при и числе степеней свободы 2 и 4}= 6, 94;

Фактическое значение критерия Fменьше табличного, следовательно .

6. Найдем по таблице критических значений двухстороннего критерия t - Стьюдента (приложение 2) значение t при уровне значимости 0,05 и числе степеней свободы v = п₁+п₂ -2 = 5+3-2=6: t_0,05=2,447.

7. Сделаем статистически значимый вывод: Поскольку t_факт.> t_0,05, нулевую гипотезу о равенстве средних в генеральных совокупностях отвергаем. Следовательно, принимаем альтернативную гипотезу о том, что средние в генеральных совокупностях не равны с вероятностью ошибки суждения 5%.

Практически значимый вывод: изучаемые сорта достоверно различаются по урожайности. Ошибка суждения составляет 5%.

2.5.3. Выборки независимые, равной численности (п₁=п₂), дисперсии в генеральных совокупностях не равны ()

Условие. Представлены выборочные данные о высоте растений подсолнечника, возделываемых по двум различным технологиям (табл.2.12).

Проверить статистическую гипотезу относительно средних величин генеральных совокупностей. Уровень значимости 0,05.

Таблица - 2.12 Высота растений подсолнечника по двум выборочным

совокупностям

Технология 1	Технология 2
единица выборки	высота растений, см	отклонение от средней	квадрат отклонения	единица выборки	высота растений, см	отклонение от средней	квадрат отклонения
	x 1 i				x 2 i
	18,6	-0,6	0,36		16,2	+0,2	0,04
	19,8	+0,6	0,36		15,9	-0,1	0,01
	20,6	+1,4	1,96		15,6	-0,4	0,16
	17,8	-1,4	1,96		16,3	+0,3	0,09
Итого	76,8	-	4,64	Итого	64,0	-	0,30

Решение

1) Выдвинем нулевую и альтернативную гипотезы:

Н₀: При разных технологиях высота средняя растений одинакова

Н_А: При разных технологиях высота средняя растений различна

2. Рассчитаем средние величины по выборкам:

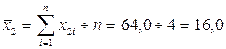(см); (см)

3. Вычислим выборочные дисперсии:

;

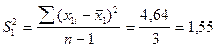4. Определим обобщенную среднюю ошибку двух выборочных средних:

(см)

5. Рассчитаем фактическое значение критерия t:

t_факт. =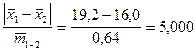

6. Для характеристики независимых выборок с точки зрения их формирования выясним равенство дисперсий в генеральных совокупностях. С этой целью проведем проверку гипотез по критерию F- распределения.

Н₀ : ; Н_А: .

F_факт.= где s₁²>s₂² F_факт.= ;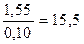

F _{при и числе степеней свободы 3 и 3}= 9,28;

Фактическое значение критерия Fменьше табличного, следовательно .

7.Определим число степеней свободы вариации с учетом того, что дисперсии в генеральных совокупностях неравны:

7. По таблице критических значений двухстороннего критерия t-Стьюдента (приложение 2) найдем значение t при и : t_0,05 = 3,182

8. Сделаем вывод. Фактическое значение критерия Стьюдента(t_факт.=5,0) больше его критического значения (t_0,05=3,18). Следовательно, фактическое значение t находится в области критических значений, и нулевая гипотеза о равенстве средних в генеральных совокупностях отвергается. Принимается альтернативная гипотеза с вероятностью ошибки суждения 5%. Практически значимый вывод: высота растений подсолнечника существенно зависит от технологии возделывания культуры. Уровень ошибки суждения 5%.

2.5.4. Выборки независимые, разной численности (п ₁ ≠ п ₂), дисперсии в генеральных совокупностях не равны ()

Условие. Представлены данные о живой массе потомства двух быков в возрасте 18 мес. (табл.2.13).

Проверить статистическую гипотезу относительно средних величин генеральных совокупностей. Уровень значимости 0,05.

2.13. Живая масса потомства двух быков – производителей, кг

Бык Андрос	Бык Лидо
единица выборки	масса, кг	отклонение от средней	квадрат отклонения	единица выборки	масса, кг	отклонение от средней	квадрат отклонения
	x 1 i				x 2 i
		-64,5	4160,25			17,6	309,76
		-19,5	380,25			19,6	384,16
		-17,5	306,25			-7,4	54,76
		101,5	10302,25			-27,4	750,76
	-	-	-			-2,4	5,76
Итого							1505,2

Решение

1.Выдвинем нулевую и альтернативную гипотезы:

Н₀: Средняя живая масса потомства двух быков равна

Н_А: Средняя живая масса потомства двух быков не равна.

2.Рассчитаем средние величины по выборкам:

(кг); (кг)

3.Вычислим выборочные дисперсии:

4. Определим обобщенную среднюю ошибку двух выборочных средних:

5.Рассчитаем фактическое значение критерия t:

t_факт. =

6. Проведем проверку гипотезы о равенстве дисперсий в генеральных совокупностях с целью определения условий формирования выборок с разной численностью.

Н₀ : ; Н_А: .

F_факт.= где s₁²>s₂² F_факт.= ;

F _{при и числе степеней свободы 3 и 4}= 6,59;

Фактическое значение критерия F больше табличного, следовательно .

Таким образом, делаем заключение о формировании выборок: п ₁ ≠ п ₂; .

7. Табличное значение критерия t-Стьюдента определяется как средняя взвешенная из табличных значений t-Стьюдента для отдельных выборок. В качестве весов выступают квадраты средних ошибок выборок:

t =

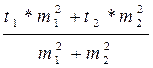
где t_{1 (при V1=3, 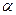=0,05)} = 3,1825 и t_{2 (V2=4, 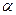=0,05)} = 2,7764_,

;

t =

8.По таблице критических значений двухстороннего критерия t-Стьюдента (приложение 2) найдем значение t при и : t_0,05 = 3,182

9.Сделаем вывод: Фактическое значение критерия Стьюдента(t_факт.=3,22) больше его критического значения (t_0,05=3,16). Следовательно, фактическое значение t находится в области критических значений, и нулевая гипотеза о равенстве средних в генеральных совокупностях отвергается, альтернативная гипотеза принимается с вероятностью ошибки суждения 5%.

Практически значимый вывод: мясная продуктивность крупного рогатого скота существенно зависит от генетического фактора. Уровень ошибки суждения 5%.

Задача 2.6 Проверка статистических гипотез относительно средней разности при парной зависимости между единицами совокупности

Условие. Имеются данные выборочного наблюдения продуктивности коров-матерей и коров-дочерей (табл.2.14).

Проверить статистическую гипотезу относительно средней разности между попарно связанными единицами генеральной совокупности. Уровень значимости 0,05.

Таблица -2.14. Продуктивность коров-матерей и коров-дочерей

Номер пары	Надой на 1 корову за год (ц)	Разность надоев (ц)	Квадрат разности надоев
матери	дочери
	х1i	x2i	di=	di2
	48,2	54,6	-6,4	40,96
	42,0	43,1	-1,1	1,21
	49,8	51,2	-1,4	1,96
	38,9	45,1	-6,2	38,44
	50,6	53,7	-3,1	9,61
Итого	-	-	-18,2	92,18

Решение.

1. Сформулируем нулевую и альтернативную гипотезы:

Н₀: Надой коров-дочерей не зависит от надоев коров-матерей.

Н_А: 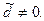Надой коров-дочерей зависит от надоев коров-матерей

2. Определим среднюю разность по данным выборки:

(ц)

3. Исчислим дисперсию средней разности:

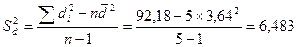
4. Рассчитаем ошибку средней разности:

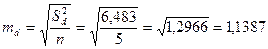
5. Вычислим фактическое значение критерия t:

t_факт.=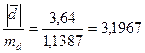

6. Найдем по таблице критических значений двухстороннего критерия t-Стьюдента (приложение 2) значение t при уровне значимости 0,05 и числе степеней свободы вариации V= n-1=4: t_0,05=2,776.

7.Сделаем статистический вывод: Фактическое значение t_факт.=3,2 больше его критического значения (t_0,05=2,78). Поэтому нулевую гипотезу о равенстве средней разности между попарно связанными наблюдениями в генеральной совокупности нулю отвергаем и принимает альтернативную гипотезу. Вероятность ошибки суждения 5%.

8. Практически значимый вывод: Продуктивность коров- матерей достоверно влияет на надой коров-дочерей. Ошибка суждения 5%.

Вопросы для проверки знаний по модулю 2:

1. Какая совокупность называется выборочной?.. генеральной?

2. Каково содержание выборочного метода?

3. Какие способы отбора единиц из генеральной совокупности в выборочную Вам известны?

4. Какие ошибки выборки могут иметь место при проведении выборочного наблюдения?

5. Какие ошибки нельзя исключить при применении выборочного метода?

6. Какие ошибки называются ошибками репрезентативности?

7. Каково содержание оценки?

8. В чем состоит свойство несмещенности оценки?

9. В чем суть точечной оценки параметра генеральной совокупности?

10. В чем суть интервальной оценки параметра генеральной совокупности?

11. Что следует понимать под «статистической гипотезой»?

12. Какова последовательность проведения проверки статистической гипотезы?

13. Какие гипотезы проверяются с использованием критерия в качестве критерия согласия?

14. Какая нулевая гипотеза выдвигается при проверке гипотезы о соответствии фактического распределения ожидаемому?

15. От чего зависит табличное значение критерия при использовании его в качестве критерия согласия?

16. В каком случае критерий используется как критерий однородности?

17. Как формулируется нулевая гипотеза при применения критерия как критерия независимости?

18. При каком аспекте использования критерия при расчете его фактического значения не используются ожидаемые (теоретические численности)?

19. От каких величин зависит, главным образом, фактическое значение критерия при использовании его в области применения как критерия независимости?

20. Как установить число степеней свободы при нахождении табличного значения критерия как критерия однородности?

21. В чем разница между выборками зависимыми и независимыми?

22. Как формулируется нулевая гипотеза о средних при независимых выборках?

23. Какие четыре ситуации возможны при проверке гипотезы относительно двух средних при независимых выборках?

24. В чем особенность расчета числа степеней свободы при неравных дисперсиях?

25. Что такое НСР?

26. Как формулируется нулевая гипотеза при зависимых выборках?

27. Каков алгоритм расчета фактического значения критерия при зависимых выборках?

28. С какой целью при проверке гипотезы относительно 2-х средних используется критерий F-Фишера? Каковы особенности проверки гипотезы в случае Fфакт.> Fтабл.?

29. Найти табличное значение критерия, если по двум вариантам обработки почвы полученны следующие значения урожайности проса:

Выборки зависимые.

30. При неизменных дисперсиях S21, S22 в каком случае большая вероятность принять нулевую гипотезу ( 1= 2) при боьших или при малых выборках и почему?

31. Вы доказали, что справедлива альтернативная гипотеза Н1: 1 2. Какова вероятность ошибочности такого вывода? Р=0,99.

32. По двум вариантам эксперимента получены средние 1=10, 2=20. Есть ли смысл в статтистической оценке различий между средними. Если есть, то почему?

33. Найти разницу между выборочными средними, если tфакт.=5, m1-2=8.

[*] Несмещенную оценку дисперсии необходимо рассчитывать, прежде всего, для совокупностей менее 30 единиц

Не нашли, что искали? Воспользуйтесь поиском: