Алгоритм построения наилучшего многочлена по данному методу

Возьмем многочлен k-ой степени

и выведем правило нахождения его наилучших коэффициентов. На самом деле, значение k не влияет па способ решения задачи, но при­веденные ниже рассуждения полезны в чисто практическом плане.

Если взять k ≥ n, то наименьшее значение уклонений дают интерполяционные многочлены, ибо для них при всех i = 0, 1,..., n. При k = n такой многочлен единственный, а при k > n их бесконечное множе­ство. Будем считать k < п. Независимо от количества табличных данных на прак­тике обычно ограничиваются многочленами степени не выше трех.

Сумма квадратов уклонений для многочлена представля­ет собой неотрицательную функцию от переменных а₀,…, а_k, обо­значим ее через F:

Требующиеся нам наилучшие коэффициенты многочлена долж­ны давать минимум функции F. Из курса математического анализа известно, что необходимым условием экстремума дифференцируемой функции многих переменных является равенство нулю ее частных производных по всем переменным. Вычислим их и приравняем нулю:

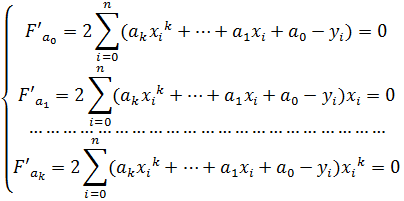
Проведя суммирование, собрав коэффициенты при а₀,…, а_k ипе­ренеся не содержащие их суммы в правую часть, получим систему линейных уравнений относительно неизвестных а₀,…, а_k:

Обозначим

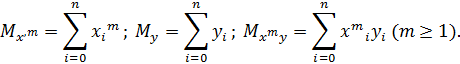
и перепишем систему в виде

Пусть решением системы является вектор ( ), который дает наименьшее значение для сумма квадратов уклонений, т.е. является точкой минимума функции F. Это означает, что из всех многочленов k -ойстепени многочлен

будет самым хорошим приближением к рассматриваемой нами таб­личной функции (по методу наименьших квадратов).

Не нашли, что искали? Воспользуйтесь поиском: