Уклонения, среднеквадратичное уклонение

Пусть в результате экспериментов получена табл.1 с произволь­ным расположением аргументов. Аналитическое выражение таблич­ной функции f может быть неизвестным. На основе этой таблицы требуется найти формулу , приближенно описывающую за­висимость между экспериментальными данными таблицы.

Полученное для этой цели соотношение у = р(х) называется эм­пирической формулой, а функция p — эмпирической функцией.

Не будем требовать от функции p обя­зательного выполнения равенств ρ 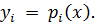Главное, чтобы она была достаточно простой, учитывала характер табличной функции и в точках х_i имела близкие к у_i значения при всех i = 0, 1,..., n.

Поиск эмпирической формулы начинается с определения клас­са функций, которые лучше всего отражают связь между табличны­ми данными. Эффективным методом для этого являются графичес­кие соображения. На координатной плоскости отмечаются определяемые данной таблицей точки, а затем по характеру их расположе­ния подбирается вид приближения из числа известных элементар­ных функций. На рис. 7 вблизи точек некоторой таблицы проведена линия у = р(х), напоминающая часть квадратной параболы. В этом случае искомой эмпирической формулой будет при неко­торых значениях коэффициентов а, b, с. Как видно из рисунка, для данной таблицы можно выбрать и более простое приближение в виде линейной функции у= ах+ b.

Пусть тип эмпирической формулы у = р(х) выбран, причем, как мы заметили, функция p на самом деле зависит от одного или не­скольких числовых параметров. Чтобы найти функцию из выбран­ного класса, график которой в каком-либо смысле ближе всех рас­положен к табличным точкам, надо определить соответствующие значения этих параметров. Возьмем в качестве меры близости функций p и f на отрезке [ x₀; x_n ]«рас­стояние» между ними и наилучшей функцией будем считать ту, для которой имеет наименьшее значение.

При определении «расстояния» ρ будем пользоваться евклидо­вым расстоянием между векторами-значениям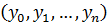и и .

Числа называют уклонениями, а вычисленное по фор­муле данной формуле «расстояние» — среднеквадратичным уклонением функции ρ от табличной функции f на отрезке [ x₀; x_n ].Абсолютные величины уклонений равны дли­нам отрезков между точками [ x_i ; y_i ]и соответствующими точ­ками графика у=р(х) (на рис. 7 эти отрезки отмечены сплошными вертикальными линиями).

Ясно, что задача минимизации «расстояния» сводится к минимизации подкоренного вы­ражения.

Задание

По данной таблице найдите многочлен второй степени 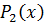являющийся наилучшим приближением к соответствующей таблич­ной функции по методу наименьших квадратов. Начертите графики таблицы и найденного многочлена. Найдите все уклонения от таб­личных значений и среднеквадратичное уклонение.

Задание по вариантам

Не нашли, что искали? Воспользуйтесь поиском: