
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Обратное линейное интерполирование
Дано какое-то значение у функции f, не равное табличным значениям  и необходимо найти соответствующий аргумент
и необходимо найти соответствующий аргумент 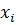 , обозначим его как
, обозначим его как  Если f монотонна в области вычисления, то обратная для нее функция там существует, причем она табличная.
Если f монотонна в области вычисления, то обратная для нее функция там существует, причем она табличная.
Формула обратного линейного интерполирования

Для вычислений с ее помощью при заданном у выбираются два соседних табличных значения функции f, между которыми находится у, и предыдущее значение принимается за  , а последующее — за
, а последующее — за  .
.
Остаточный член данной формулы выглядит следующим образом:

где с — некоторое число между  . Следовательно,
. Следовательно,

где 
Общая оценка погрешности формулы для всех у, находящихся между  , обеспечивается неравенством
, обеспечивается неравенством

Задание
Дана таблица значений функции  с верными цифрами:
с верными цифрами:
| x | 
| X | 
| X | 
| X | 
| X | 
|
| 0,4 | 1,1024 | 0,8 | 1,5082 | 1,2 | 2,3881 | 1,6 | 3,9536 | ||
| 0,1 | 1,0053 | 0,5 | 1,1693 | 0,9 | 1,6763 | 1,3 | 2,7057 | 1,7 | 4,4823 |
| 0,2 | 1,0227 | 0,6 | 1,2575 | 1,0 | 1,8768 | 1,4 | 3,0696 | 1,8 | 5,0758 |
| 0,3 | 1,0543 | 0,7 | 1,3695 | 1,1 | 2,1130 | 1,5 | 3,4842 | 1,9 | 5,7396 |
| Вариант | а | b | с | d |
| 0,96 | 0,92 | 1,2775 | 1,0049 |
Все исходные данные a, b, c, d считаются точными числами.
1. Вычислим приближенное значение  с помощью первого интерполяционного многочлена Ньютона второй степени, определим его абсолютную погрешность и верные значащие цифры.
с помощью первого интерполяционного многочлена Ньютона второй степени, определим его абсолютную погрешность и верные значащие цифры.

Составим таблицу конечных разностей:
| x | y | Δ y | Δ2 y | Δ3 y | Δ4 y |
| 0,0053 | 0,0121 | 0,0021 | 0,0002 | ||
| 0,1 | 1,0053 | 0,0174 | 0,0142 | 0,0023 | |
| 0,2 | 1,0227 | 0,0316 | 0,0165 | 0,0023 | 0,0002 |
| 0,3 | 1,0543 | 0,0481 | 0,0188 | 0,0025 | |
| 0,4 | 1,1024 | 0,0669 | 0,0213 | 0,0025 | 0,0004 |
| 0,5 | 1,1693 | 0,0882 | 0,0238 | 0,0029 | -0,0002 |
| 0,6 | 1,2575 | 0,112 | 0,0267 | 0,0027 | 0,0003 |
| 0,7 | 1,3695 | 0,1387 | 0,0294 | 0,003 | 0,0003 |
| 0,8 | 1,5082 | 0,1681 | 0,0324 | 0,0033 | -0,0001 |
| 0,9 | 1,6763 | 0,2005 | 0,0357 | 0,0032 | 0,0004 |
| 1,8768 | 0,2362 | 0,0389 | 0,0036 | 0,0002 | |
| 1,1 | 2,113 | 0,2751 | 0,0425 | 0,0038 | 0,0006 |
| 1,2 | 2,3881 | 0,3176 | 0,0463 | 0,0044 | -0,0003 |
| 1,3 | 2,7057 | 0,3639 | 0,0507 | 0,0041 | 0,0004 |
| 1,4 | 3,0696 | 0,4146 | 0,0548 | 0,0045 | 0,001 |
| 1,5 | 3,4842 | 0,4694 | 0,0593 | 0,0055 | |
| 1,6 | 3,9536 | 0,5287 | 0,0648 | 0,0055 | |
| 1,7 | 4,4823 | 0,5935 | 0,0703 | ||
| 1,8 | 5,0758 | 0,6638 | |||
| 1,9 | 5,7396 | ||||
| Табл. 3 |
Поскольку вторые разности таблицы практически постоянны, хорошее приближение должен дать многочлен второй степени. Используя данные девятой строки табл.3, на отрезке [0,9; 1,0] будем иметь интерполяционную формулу

Оценим погрешность этой формулы в точке  . Поскольку
. Поскольку  для всех
для всех  , примем
, примем  . Учитывая значение t = 0,6, находим
. Учитывая значение t = 0,6, находим

Таким образом, при  погрешность интерполяции меньше погрешности таблицы
погрешность интерполяции меньше погрешности таблицы  , поэтому точность результата определится точностью табличных данных. Чтобы узнать степень влияния этих данных, сначала вычислим
, поэтому точность результата определится точностью табличных данных. Чтобы узнать степень влияния этих данных, сначала вычислим 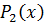 :
:

а затем найдем оценку υ точности приближения  . Для этого применим правила учета погрешностей арифметических действий, имея в виду, что число
. Для этого применим правила учета погрешностей арифметических действий, имея в виду, что число  здесь точное. Абсолютные погрешности табличных данных определим по верным цифрам значений уi:
здесь точное. Абсолютные погрешности табличных данных определим по верным цифрам значений уi:
у чисел уi они равны 0,0005, у разностей Δ yi — 0,001, у Δ2 yi — 0,002. Тогда

Полученная оценка ν действительно является основной в суммарной оценке погрешности приближения 1,7923 к  :
:

Теоретически число 1,7923 имеет только две верные значащие цифры после запятой. Для сравнения приведем искомое значение функции с пятью верными значащими цифрами, рассчитанное на калькуляторе:  . Расстояние
. Расстояние 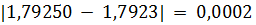 показывает, что при учете вычислительной погрешности получена завышенная ее оценка (в основном за счет завышения оценок погрешностей значений уi и конечных разностей по сравнению с их реальными погрешностями). На самом деле верными являются три цифры после запятой.
показывает, что при учете вычислительной погрешности получена завышенная ее оценка (в основном за счет завышения оценок погрешностей значений уi и конечных разностей по сравнению с их реальными погрешностями). На самом деле верными являются три цифры после запятой.
Ответ:  .
.
2. Линейным интерполированием найдите значения функции f для аргументов  и определите их верные значащие цифры с помощью таблицы конечных разностей.
и определите их верные значащие цифры с помощью таблицы конечных разностей.

Поскольку  для всех
для всех  , примем
, примем  . Сначала применим общие для всех
. Сначала применим общие для всех  неравенства оценки погрешностей:
неравенства оценки погрешностей:

Так как Δ2y=0,0357 (из табл. 3),

Обе оценки почти одинаковы и показывают, что не только числам а и b, но и всем другим приближениям к функции, для всех  , формула обеспечивает по крайней мере две верные значащие цифры после десятичной запятой.
, формула обеспечивает по крайней мере две верные значащие цифры после десятичной запятой.
Из оценочной функции
1) для  :
: 

2) для 

Следовательно, в обоих случаях формула даст нам две верные цифры. Найдем искомые приближения:


Для оценки точности вычислений определяем абсолютные погрешности чисел у0 =  и Δ у0 = 0,042 по известным верным цифрам табличных значений
и Δ у0 = 0,042 по известным верным цифрам табличных значений

Точность значения Р1(1,11) оценится числом ν = 0,0005 + 0,1 · 0,001 = 0,0006.
Добавляем 0,00006 к подсчитанной ранее оценке

Значит, у a и b будет две верные цифры после запятой.


3. Вычислим значения обратной для d функции φ для аргументов с, d по формуле обратного линейного интерполирования и запишите ответы с двумя цифрами после десятичной запятой.
1) Для 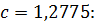

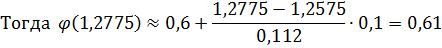
2) Для  :
:




Не нашли, что искали? Воспользуйтесь поиском: