
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение шага разбиения отрезка интегрирования, при
котором квадратурная формула обеспечивает заданную точность
При решении задачи численного интегрирования с заданной точностью 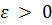 необходимо найти
необходимо найти  так, чтобы оказалось
так, чтобы оказалось  . Для этого допустимую погрешность обычно делят между двумя источниками с учетом степени их влияния на результат:
. Для этого допустимую погрешность обычно делят между двумя источниками с учетом степени их влияния на результат: 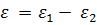 . Сначала определяют число п, удовлетворяющее неравенству
. Сначала определяют число п, удовлетворяющее неравенству  , что равносильно выбору такого шага разбиения, при котором квадратурная формула обеспечивает точность
, что равносильно выбору такого шага разбиения, при котором квадратурная формула обеспечивает точность  Затем при найденном n вычисляют значение
Затем при найденном n вычисляют значение 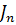 с точностью до
с точностью до 
Ясно, что в случае хорошо вычисляемых функций /надо выбирать  существенно меньшим, чем
существенно меньшим, чем  . Это позволит сократить объем вычислений за счет уменьшения количества разбиений отрезка
. Это позволит сократить объем вычислений за счет уменьшения количества разбиений отрезка  .
.
Из следующих неравенств можно вычислить 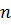 – количество отрезков разбиения:
– количество отрезков разбиения:
1) Формула трапеций:
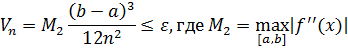
2) Формула Симпсона:

Вопросы оценки точности приближенного интеграла с учетом вычислительных погрешностей
Так как интеграл отыскивается посредством двух приближенных равенств 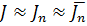 поскольку точные значения функции f обычно неизвестны и поэтому удается найти лишь приближенное значение
поскольку точные значения функции f обычно неизвестны и поэтому удается найти лишь приближенное значение 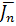 выражения
выражения 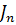 . При этом часто возникает ситуация, когда узлы
. При этом часто возникает ситуация, когда узлы 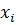 приходится брать с округлением. Естественно, что погрешности
приходится брать с округлением. Естественно, что погрешности 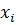 также повлияют на точность
также повлияют на точность 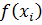 .
.
В результате сложения погрешностей квадратурной формулы и вычисления значения 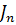 образуется погрешность числа
образуется погрешность числа 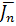 относительно точного интеграла
относительно точного интеграла  . Пусть
. Пусть  — оценка погрешности вычисления
— оценка погрешности вычисления  . Тогда абсолютная погрешность приближенного интеграла
. Тогда абсолютная погрешность приближенного интеграла 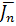 относительно
относительно 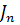 определяется по формуле
определяется по формуле

Степень влияния двух отмеченных источников погрешностей на результат зависит от подынтегральной функции.
Если f задана аналитически и 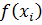 .можно находить с любой точностью, основное внимание обращают на погрешность квадратурной формулы. Тогда при каждом
.можно находить с любой точностью, основное внимание обращают на погрешность квадратурной формулы. Тогда при каждом 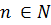 вычисления с достаточно большим количеством цифр обеспечат незначительность
вычисления с достаточно большим количеством цифр обеспечат незначительность  по сравнению с
по сравнению с 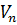 .
.
Другой крайний случай возникает в ситуации, когда нет ограничений на количество точек разбиения отрезка интегрирования, но 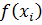 находятся с малой точностью, например экспериментальным путем. Тогда на первое место выходит задача учета погрешностей вычислений.
находятся с малой точностью, например экспериментальным путем. Тогда на первое место выходит задача учета погрешностей вычислений.
Оба источника существенны, если данные для квадратурных формул берутся из таблицы значений подынтегральной функции, ибо тогда точность вычислений ограничена точностью таблицы, а точность формулы — шагом таблицы.
Задание
| Вариант | Интеграл |

|
1. Вычислите данный интеграл вручную по формуле трапеций при n = 3 и n = 6. Оцените погрешность приближения J6(T) методом двойного пересчета, а затем найдите абсолютную погрешность этого же приближения по формуле строгой оценки погрешностей.
1) 
| x | 0,667 | 1,333 | ||
| y | 0,841 | 0,995 | 0,723 | 0,141 |

1) 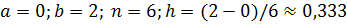
| x | 0,333 | 0,666 | 0,999 | 1,333 | 1,666 | ||
| y | 0,841 | 0,972 | 0,995 | 0,910 | 0,723 | 0,458 | 0,141 |


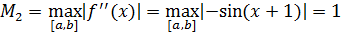
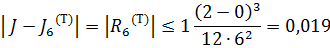
Погрешность вычислений

Абсолютная погрешность
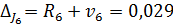
Следовательно, у  одна верная цифра после запятой.
одна верная цифра после запятой.
2. Вычислим данный интеграл по формуле Симпсона с точностью до  , для чего сначала надо определим число п, при котором формула обеспечивает точность ε, затем составим программу реализации формулы и с ее помощью найдем
, для чего сначала надо определим число п, при котором формула обеспечивает точность ε, затем составим программу реализации формулы и с ее помощью найдем 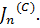 Для того чтобы не учитывать вычислительные погрешности, шаг разбиения и значения функций возьмем с двумя запасными цифрами, тогда пусть
Для того чтобы не учитывать вычислительные погрешности, шаг разбиения и значения функций возьмем с двумя запасными цифрами, тогда пусть  .
.


Составим программу реализации формулы и с ее помощью найдем  . Текст программы:
. Текст программы:
var a,b,h,x:real;
n,i:integer;
integ:real;
function F(x:real):real;
begin
F:=sin(x+1)
end;
begin
write('a='); readln(a);
write('b='); readln(b);
write('n='); readln(n);
if (n mod 2)>0 then
begin
n:=n+1;
writeln('4islo n bylo vvedeno ne4etnoe, ono zameneno na',n);
end;
h:=(b-a)/n;
integ:=F(a)+F(b)+4*F(a+h);
for i:=1 to (n div 2)-1 do
begin
x:=a+2*h*i;
integ:=integ+2*F(x)+4*F(x+h);
end;
integ:=h*integ/3;
writeln('integral = ',integ:1:6);
readln;
end.
Результат, выведенный на экран (возьмем также n=8 для  )
)
a=0
b=2
n=26
integral = 1.530295
a=0
b=2
n=8
integral = 1.530328
Ответ: 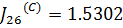
3. Вычислите интеграл по формуле Ньютона-Лейбница с максимальной точностью, которая возможна при используемых вычислительных средствах.

6. Сравните полученные разными способами результаты по их точности.
Так как интеграл выражается через элементарные функции, то наиболее точным значением будет то, что рассчитано по формуле Ньютона-Лейбница. Расчет по формуле трапеций требует большого количества шагов разбиения для обеспечения высокой точности; формула Симпсона же, напротив, позволяет добиться высокой точности, не прибегая к уменьшению отрезка шага разбиения.
Не нашли, что искали? Воспользуйтесь поиском: