Задача Коши. Теорема Пикара

Задача нахождения частного решения уравнения , удовлетворяющего начальному условию у=у₀ и x=х₀, на­зывается задачей Коши.

Задачу Коши можно решить без выявления общего решения. Если же общее решение известно и начальное условие дано, то число С ₀, определяющее искомое частное решение, нахо­дят из уравнения относительно .

Геометрический смысл задачи Коши заключается в нахождении интегральной кривой, проходящей через начальную точку (х₀, у₀).

Преж­де чем приступать к решению задачи Коши, предварительно надо выяснить, существует ли решение уравнения, удовлетворяющее дан­ному начальному условию, а если да, то сколько их может быть. Справедлива следующая теорема (теорема Пикара): пусть точка (х₀, у₀) является внутренней точкой замкнутой прямоугольной области

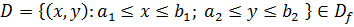
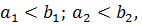и на области D выполнены условия:

1) функция f непрерывна как функция двух переменных;

2) частная производная f'_y существует и ограничена как функция двух переменных (в частности, непрерывна в этой области).

Тогда найдется такой отрезок 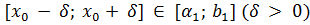, на котором уравнение имеет единственное решение удов­летворяющее заданному начальному условию.

В качестве начальной точки в теореме Пикара мож­но взять любую внутреннюю точку области D. Следовательно, че­рез каждую такую точку в достаточно малой ее окрестности прохо­дит единственная интегральная кривая из семейства .

Не нашли, что искали? Воспользуйтесь поиском: