Методом двойного пересчета

Формулы приблизительной оценки точности значений численного решения методом двойного пересчета (методом Рунге) основа­ны на учете только погрешностей усечения формулы Тейлора, т.е. при этом пренебрегают другими источниками погрешностей, вклю­чая и вычислительные.

Пусть строится таблица с отстоящими на шаг h аргументами Сначала одним из методов отыскивают значения с шагом h, а затем проводятся вычисления с шагом h/2. Понятно, что в последнем случае при каждом переходе от данного аргумента к следующему потребуется двукратное применение ме­тода. Соответствующие аргументам х_i новые табличные значения обозначим через у_i*(у₀*=у₀). Это улучшенные приближения к 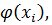и поэтому таблицу с данными возьмем в каче­стве искомого численного решения с шагом h.

Расстояния между у_i* и точными числами вы­числяются по приближенным формулам для Метода Эйлера- Коши

Задание

Используя метод Эйлера-Коши, найдите численное решение дифференциального уравнения на отрезке с шагом h = 0,1, удов­летворяющее начальному условию (в таблицу простав­лять улучшенные значения у*, найденные двукратными вычисле­ниями с шагом h/2 = 0,05). Оцените погрешности чисел у* методом двойного пересчета и определите верные значащие цифры этих чи­сел. Начертите ломаную Эйлера.

Уравнения по вариантам

Вариант	Уравнение	x0	y0
				[2;3]

Не нашли, что искали? Воспользуйтесь поиском: