
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Порядок выполнения работы. 1. Убедимся в существовании и единственности решения поставленной задачи Коши.
1. Убедимся в существовании и единственности решения поставленной задачи Коши.
Согласно теореме Пикара: точка (2, 0) является внутренней точкой замкнутой прямоугольной области 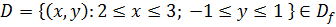 и на области D выполняются условия:
и на области D выполняются условия:
1) функция  непрерывна как функция двух переменных;
непрерывна как функция двух переменных;
2) частная производная  существует и ограничена как функция двух переменных.
существует и ограничена как функция двух переменных.
Следовательно, на отрезке  , на котором уравнение
, на котором уравнение 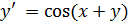 имеет единственное решение
имеет единственное решение  удовлетворяющее заданному начальному условию.
удовлетворяющее заданному начальному условию.
2. Вычислим вручную у1* и оценим его погрешность.
 , где
, где 
При h=0,1

При h=0,05

Погрешность:

3. Составим программу вывода таблицы, где у — приближение к значению точного решения в точке xi , найденное однократным вычислением по методу Эйлера-Коши (с шагом h = 0,1), Е — оценка погрешности значения у*.
Текст программы:
var a,b,x0,y0,x,y,fm,fm1,h,y1,y2:real;
i:longint;
procedure vvod;
begin
a:=2;
b:=3;
x0:=2;
y0:=0;
end;
function fun(x:real;y:real):real;
begin
fun:=cos(x+y);
end;
function vu4(h:real):real;
begin
x:=x0;
y:=y0;
repeat
begin
fm:=fun(x,y);
fm1:=fun(x+h,y+h*fm);
y:=y+h/2*(fm+fm1);
x:=x+h;
end
until x>b;
vu4:=y;
end;
procedure vyvod;
begin
writeln('Tablyca zna4eniy');
x:=x0;
y:=y0;
i:=0;
h:=0.1;
repeat
begin
write('x='); write(x:0:5,' ');
write('y='); writeln(y:0:5);
fm:=fun(x,y);
fm1:=fun(x+h,y+h*fm);
y:=y+h/2*(fm+fm1);
x:=x+h;
i:=i+1;
end
until i>(b-a)/h;
writeln;
write('4yslo iteraciy=',i-1)
end;
begin
vvod;
i:=10;
repeat
begin
h:=(b-a)/(2*i);
i:=i*2;
y1:=vu4(h);
y2:=vu4(h/2);
writeln ('y*=', y2, ' E=', (y1-y2)/3);
end;
until (abs(y1-y2))/3<0.00001;
vyvod;
writeln;
readln
end.
Результат, выведенный на экран:
y*=-0.622330289016936 E=-0.0061927127952861
y*=-0.603894765843361 E=-0.00614517439119137
y*=-0.603892097470492 E=-8.89457623184005E-07
Tablyca zna4eniy
x=2.00000 y=0.00000
x=2.10000 y=-0.04423
x=2.20000 y=-0.09318
x=2.30000 y=-0.14632
x=2.40000 y=-0.20321
x=2.50000 y=-0.26346
x=2.60000 y=-0.32670
x=2.70000 y=-0.39264
x=2.80000 y=-0.46102
x=2.90000 y=-0.53158
x=3.00000 y=-0.60413
4yslo iteraciy=10
4. Получим искомое численное решение, выписывая табличные значения с верными значащими цифрами.
| x | y |
| 2,1 | -0,4423 |
| 2,2 | -0,9318 |
| 2,3 | -0,14632 |
| 2,4 | -0,20321 |
| 2,5 | -0,26346 |
| 2,6 | -0,32670 |
| 2,7 | -0,39264 |
| 2,8 | -0,46102 |
| 2,9 | -0,53158 |
| -0,60413 |
5. Построим соответствующую ломаную Эйлера.

|
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА:
1. Исаков, В.Б. Элементы численных методов: Учебное пособие для студентов, обучающихся по специальности Математика. - М.: Академия, 2003.-192 с.: ил.
2. Демидович Б.П., Марон И.А. Основы вычислительной математики. — М.: Наука, 1970.
3. Демидович Б.П., Марон И.Α., Шувалова Э.З. Численные методы анализа. - М.: Наука, 1967.
4. Калиткин Н.Н. Численные методы. — М.: Наука, 1978.
5. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы. — М.: Просвещение, 1990.
Не нашли, что искали? Воспользуйтесь поиском: