Метод Эйлера- Коши, его геометрический смысл

⇐ Предыдущая 32 33 34 35 36 37 383940 41 Следующая ⇒

Геометрический вывод. Рассмотрим алгоритм последовательного вычисления методом Эйлера- Коши.

Пусть известны данные x_i, у_i и x_i+1. Более точное приближение можно получить, если учитывать направления интегральных кривых, характерные для начала и конца отрезка [ x_i, x_i+1 ]. Иллюстрация вычисления при i=0 приведена на рис. 10.

Точка лежит на некоторой интегральной кривой (при i=0 это точное решение задачи Коши у = φ(x)), касательная к которой в точке A_i имеет угловой коэффициент Найдемординату точки на этой касательной, соответствующей абсциссе x_i+₁ :

Вычислив , узнаем направление проходящей через 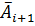интегральной кривой в этой точке. Теперь найдем «усредненное» направление кривых на рассматриваемом отрезке:

и возьмем в качестве число

Геометрический смысл этой формулы следующий. Если через исходную точку A_i провести прямую с угловым коэффициентом и взять на ней точку A_i₊₁ с абсциссой x_i+₁ то эта формула определяет ординату этой точки.

Аналитический вывод. Для простоты ограничимся получением формул при i = 0.

В основе вычислений методом Эйлера лежит линейное относительно h усечение формулы Тейлора. Можно ожидать более высокой точности от y_it если вместо линейного усечения брать квадратичное.

Имеет место равенство

из которого отбрасыванием слагаемого получим

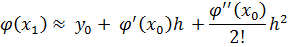
Подставим вместо его приближенное значение

наличие которого следует из определения второй производной. Тогда

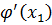Здесь известно число . Чтобы выразить через значение функции f, найдем «грубое» приближение к :

и обозначим через ψ решение уравнения , удовлетворяющее начальному условию: 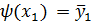. Понятно, что . Поскольку φ и ψ являются родственными решениями, можно взять

⇐ Предыдущая 32 33 34 35 36 37 383940 41 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: