Понятие численного решения. Ломаная Эйлера

…	…
Табл.2

Потребность в приближенном решении задачи Коши возника­ет прежде всего в том случае, когда дифференциальное уравнение не принадлежит ни одному из классов уравнений, для которых из­вестны точные методы интегрирования. Приближенные методы часто применяют и тогда, когда точные методы оказываются не­эффективными ввиду больших затрат времени и усилий для их реализации.

На практике наиболее распространенными являются численные методы приближенного интегрирования дифференциальных урав­нений, дающие решение задачи Коши в виде таблицы приближен­ных значений точного решения φ. Эту табли­цу [таблично заданную функцию и на­зывают численным решением задачи Коши. Для выполнения начального условия табли­ца должна содержать данные х₀, у₀.

…	…
Табл.3

Если задан конечный промежуток, на ко­тором ищется решение, и точка х₀ лежит внут­ри этого промежутка, приближенное решение имеет вид табл. 2. Вначале в ней известны х₀ и у₀, затем отыскиваются остальные таблич­ные данные. Так как правила определения «верхних» и «нижних» (относительно х₀ и у₀ ) данных одинаковы, будем искать это решение в виде табл. 3.

Для построения табл. 3 выбирается шаг h и вычисляются табличные аргументы .Затем последовательно на­ходятся числа ,близкие к значениям точно­го решения в точках :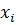

Точность приближенных равенств (5.6) зависит от способа вы­числения и от шага таблицы h. Чем меньше шаг, тем выше должна быть точность таблицы. Заданное значение у₀ считается точным чис­лом. Погрешности появляются при вычислении у₁, а далее обычно происходит их накопление.

Табл. 3 является приближением к решению φ. Если на плоскости хОу построить точки таблицы (х₀, у₀),...,(х_n, у_n) и соединить их отрезками, по­лучится так называемая ломаная Эй­лера (рис. 10). Она будет приближе­нием интегральной кривой .

Теорема. Если все частные производные функции f до k-го (k≥ 1) порядка непрерывны в прямоугольной области D, то всякое реше­ние уравнения , график которого проходит через внут­реннюю точку (х₀, у₀) этой области, имеет производную (k + 1)-го порядка, непрерывную в некоторой окрестности x₀.

Не нашли, что искали? Воспользуйтесь поиском: