Геометрический смысл правой части дифференциального

урав­нения, разрешенного относительно производной

Возьмем произвольную точку 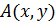на интегральной кривой (рис. 9). Так как функция φ является решением, справедливо соотношение

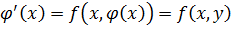
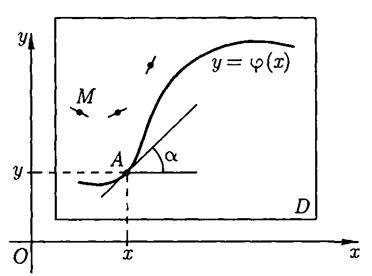С другой стороны, по геометрическому смыслу производной, 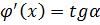, где α — угол между касательной, проведенной к дан­ной кривой в точке А, и поло­жительным направлением оси Ох. Отсюда следует, что 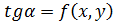,т.е. значение f(x,у) функции f равно угловому коэф­фициенту касательной, прове­денной в точке А к интеграль­ной кривой .

Полученный результат спра­ведлив для любой внутренней точки М(х,у) из области D. Вы­числив получим угловой коэффициент касательной к некоторой проходящей через эту точку интегральной кривой, при этом сама кривая может быть не­известна. Можно сказать, что значения 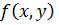определяют направ­ления интегральных кривых в тех точках, где они вычислены.

Направление кривой в точке М(х,у) обычно указывается с по­мощью отрезка небольшой длины с центром в Μ и с углом наклона 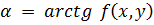к положительному направлению оси Ох. Проведя достаточно большое число таких отрезков, получаем некоторое пред­ставление о конфигурации интегральных кривых уравнения.

Не нашли, что искали? Воспользуйтесь поиском: