Базис линейного пространства и координаты вектора в базисе.

Совокупность векторов называют базисом в 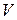, если

1^о. вектора – линейно независимы;

2^о. для 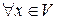найдутся 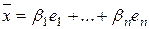. (1)

При этом равенство (1) называется разложением элемента 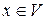по базису , а 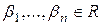называются координатами относительно базиса .

Теорема: (о единственности разложения по базису). Любой элемент 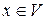может быть единственным образом разложен по базису , т.е. координаты вектора относительно базиса определяются однозначно.

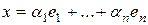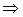
Доказательство. Пусть и . Тогда . В силу линейной независимости 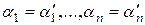. ч.т.д.

Теорема: (операции над векторами, заданными своими координатами). При сложении любых двух векторов и их координаты (относительно любого фиксированного базиса в 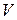) складываются; при умножении 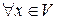на , все координаты вектора умножаются на это число.

Доказательство. Пусть - базис в 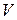, , 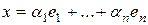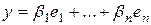. Тогда в силу аксиом линейного пространства , . В силу единственности разложения по базису 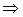что теорема доказана.

Примеры. 1^о. Базис в - любое ненулевое число.

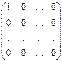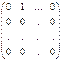2^о. . Базис образуют матрицы , , …, с одним единичным элементом.

3^о. 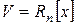– множество многочленов степени не выше n. Базис: , , …, .

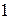Не нашли, что искали? Воспользуйтесь поиском: