Базис векторного пространства и его размерности.

Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.

Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.

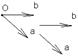
Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.

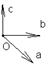
ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у наз-ся координатами вектора ОС в данном базисе

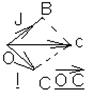
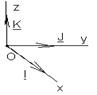
Вектора

Теорема

Система векторов A1,…..,Ak линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов этой системы.

Доказательство. Пусть система векторов линейно зависима. Тогда существует такой набор коэффициентов j1,j2,..jk, что j1*A1 + j2*A”+…jk*Ak=0, причем хотя бы один коэффициент отличен от нуля. Предположим, что A1!=0. Тогда

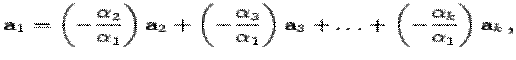
то есть A1 является линейной комбинацией остальных векторов системы.

Пусть один из векторов системы является линейной комбинацией остальных векторов. Предположим, что это вектор A1, то есть A1 = v2*A2+v3*A3+…+vk*Ak. Очевидно, что –A1+v2A2+…+vkAk=0. Получили, что линейная комбинация векторов системы равна нулю, причем один из коэффициентов отличен от нуля (равен -1).

Не нашли, что искали? Воспользуйтесь поиском: