Смешанное произведение.

Пусть в правом ортонормированном базисе i,j,k заданы векторы a = (A1,A2,A3), b = (B1,B2,B3), c = (Y1,Y2,Y3). Тогда

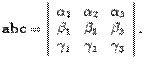
Доказательство. По предложению 10.25 находим координаты вектора b x c:

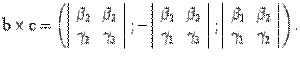
По теореме 10.3 находим скалярное произведение вектора a на вектор b x c:

Правая часть этого неравенсва совпадает с определением определителя

По определению a*b*c = a*(b x c)

Что и требовалось доказать.

Свойство дистрибутивности скалярного произведения.

a(b+c)=ab+ac;

Докажем/ В силу свойства 7:

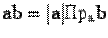
Если a!=0

имеем a(b+c) = |a|*Пр(b+c) на a. Т.к. Пр(b+c) на a=Пр b на a + Пр c на a. Поэтому

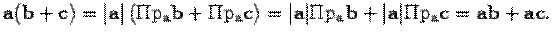
Если же а =0 то св-во очевидно.

Распределительное свойство векторного произведения.

Векторное произведение обладает свойством дистрибутивности, то есть a x (b+c)= a x b + a x c.

Доказательство. Выберем в пространстве правый ортонормированный базис i,j,k. Пусть d = a x (b+c)

d = (A,B,Y), d1=a x b, d1=(A1,B1,Y1), d2 = a x c, d2 = (A2,B2,Y2). Нам нужно доказать, что d = d1 + d2, то есть что

выполняются равенства: A = A1 + A2, B = B1 + B2.

Т.к. Проекции вектора на координатные оси равны коодинатам вектора, то

По свойству линейности смешанного произведения

Аналогично доказываются равенства B = B1 + B2, Y = Y1 + Y2.

Не нашли, что искали? Воспользуйтесь поиском: