Следующее предложение показывает геометрический смысл смешанного произведения.

Смешанное произведение abc некомпланарных векторов равно объему параллелепипеда, сторонами которого служат векторы a,b,c, взятому со знаком " + ", если векторы образуют правую тройку, и со знаком " - ", если -- левую.

Доказательство. Пусть d = b x c. По предложению 10.22 |d| равен площади S параллелограмма, сторонами которого служат векторы b,c (рис. 10.26, 10.27).

По свойству 7 скалярного произведения (теорема 10.2)

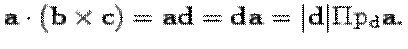
Пусть h -- высота параллелепипеда (рис. 10.26, 10.27). Если a,b,c -- правая тройка векторов, то Пр a(на d) =h (рис. 10.26),

Если a,b,c -- левая тройка, то Пр а(на d) = -h. Так как S*h=V -- объем параллелепипеда, то из формулы (10.7) получим

Abc=V в случае правой тройки и abc= -V в случае левой тройки сомножителей.

Заметим, что если тройка векторов a,b,c является правой, то тройки c,a,b и b,c,a также будут правыми, а тройки b,a,c, c,b,a и a,c,b будут левыми тройками векторов.

Так как объем параллелепипеда не зависит от того, в каком порядке перечисляются его стороны, то abc=cab=bca=-bac=-cba=-acb

Не нашли, что искали? Воспользуйтесь поиском: