
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
О выполнении типового расчЕта
Н.П. Бородин
В.В. Жернова
Л.В. Шуметова
В.С. Шоркин
РЯДЫ



министерство образования российской федерации
орловский государственный технический университет
Н.П. Бородин, В.В. Жернова, Л.В. Шуметова,
В.С. Шоркин
РЯДЫ
Рекомендовано редакционно-издательским советом ОрелГТУ
в качестве учебно-методического пособия
Орел 2004
УДК 517.52(076)
ББК 22.1613я7
Б83
Рецензенты:
заведующий кафедрой высшей математики ОрелГТУ,
доктор технических наук, профессор
В.А. Гордон,
заведующий кафедрой геометрии и методики преподавания
математики ОГУ, кандидат педагогических наук, профессор
В.В. Ветров
Б83 Бородин Н.П. Ряды: Учебно-методическое пособие / Н.П. Бородин, В.В. Жернова, Л.В. Шуметова, В.С. Шоркин. – Орел:
ОрелГТУ, 2004. – 39 с.
В учебно-методическом пособии по выполнению типового расчета «Ряды» даются подробные решения задач с полным анализом. Пособие предназначено студентам технических специальностей. Предлагаемый материал окажет большую помощь студентам в самостоятельном освоении курса высшей математики, особенно при подготовке к практическим занятиям, контрольным работам и при выполнении типовых расчетов.
УДК 517.52(076)
ББК 22.1613я7
© ОрелГТУ, 2004
© Бородин Н.П., Жернова В.В.,
Шуметова Л.В., Шоркин В.С., 2004
СОДЕРЖАНИЕ
Введение............................................................................................................. 4
1 О выполнении типового расчета................................................................ 5
1.1 О рядах...................................................................................................... 6
2 Числовые ряды.............................................................................................. 8
2.1 Сумма ряда............................................................................................... 8
2.2 Свойства сходящихся рядов............................................................... 12
2.3 Необходимый признак сходимости ряда.......................................... 13
2.4 Достаточные признаки сходимости рядов с положительными
членами.................................................................................................... 13
2.4.1 Признак сравнения........................................................................... 13
2.4.2 Признак Даламбера.......................................................................... 14
2.4.3 Признак Коши.................................................................................. 14
2.4.4 Интегральный признак Коши........................................................ 15
2.5 Знакопеременные ряды........................................................................ 18
3 Функциональные ряды.............................................................................. 21
3.1 Равномерная сходимость функционального ряда........................... 25
3.2 Признак Вейерштрасса......................................................................... 27
3.3 Интегрирование и дифференцирование степенных рядов............. 29
4 Ряд Тейлора................................................................................................. 34
4.1 Приближенное вычисление интегралов с помощью степенных
рядов........................................................................................................ 36
5 Вопросы для самопроверки...................................................................... 37
Список рекомендуемой литературы........................................................... 38
ВВЕДЕНИЕ
Последние несколько лет работы высшей школы нашей страны отмечены значительным уменьшением объёма часов, отводимых действующими учебными планами на чтение лекций и проведение семинарских и практических занятий. В связи с присоединением нашей страны к Болонскому соглашению указанная выше тенденция будет усиливаться. В этих условиях возникает проблема: как организовать изучение вузовских дисциплин студентами, в частности математики, чтобы знания студентов были не хуже, чем это было в советское время. Одним из путей решения этой проблемы, безусловно, является совершенствование форм самостоятельной работы студентов. Авторы настоящего пособия на основе системы типовых заданий (на основе типовых расчетов) разработали учебно-методический комплекс, который позволяет занять студентов разноуровневой самостоятельной работой, начиная от репродуктивной и кончая продуктивной или даже творческой. У преподавателей, таким образом, появляется возможность пойти на дальнейшее сокращение аудиторных часов, а освободившееся время употребить на повышение своей квалификации, на контроль самостоятельной работы студентов, на проведение для них консультаций.
Пособие написано в полном соответствии с программой по изучению высшей математики в технических вузах. Следует отметить, что решения задач № 1, 2, 4, 5, 6, 8, 9, 12, 14, 19, 20 связаны в основном с формированием у студентов знаний 3-го уровня – продуктивного. Остальные, более трудные – это задачи творческого характера (4-й уровень).
Студенту, прежде чем решать задачи типового расчета по задачнику Л.А. Кузнецова, необходимо изучить соответствующий раздел теории, а затем внимательно, с выполнением всех действий на бумаге разобрать решенные задачи нашего пособия. Пособие может быть полезно и для преподавателей, ведущих практические занятия.
О выполнении типового расчЕта
При выполнении типового расчета следует пользоваться рекомендуемой литературой (см. с. 38).
Чтобы выполнить теоретические упражнения, мы даем некоторые указания, включающие ссылки на отдельные главы и страницы учебников.
Упражнение 1
Ряды  и
и  сходятся. Доказать,что ряд
сходятся. Доказать,что ряд  сходится, если
сходится, если  .
.
Литература: [1, гл. 4], [2, гл. 9].
Упражнение 2
Ряд  (
( ) сходится. Доказать, что ряд
) сходится. Доказать, что ряд  тоже сходится. Показать, что обратное утверждение неверно.
тоже сходится. Показать, что обратное утверждение неверно.
Литература: [1, гл. 4], [2, гл. 9, с. 366].
Упражнение 3
Ряды  и
и  сходятся. Доказать, что ряд
сходятся. Доказать, что ряд 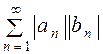 тоже сходится.
тоже сходится.
Указание. В доказательстве следует применить неравенство  .
.
Литература: [1, гл. 4, с. 418, 423], [2, гл. 9].
Упражнение 8
Показать, что функция  всюду непрерывна.
всюду непрерывна.
Указание. Докажите равномерную сходимость ряда  , пользуясь признаком Вейерштрасса, и непрерывность его членов. Если ряд будет сходиться равномерно всюду, то функция
, пользуясь признаком Вейерштрасса, и непрерывность его членов. Если ряд будет сходиться равномерно всюду, то функция 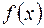 будет всюду непрерывной.
будет всюду непрерывной.
Литература: [5, гл. 12].
Упражнение 9
Доказать, что ряд  сходится равномерно в интервале
сходится равномерно в интервале  . Можно ли его почленно дифференцировать в этом интервале?
. Можно ли его почленно дифференцировать в этом интервале?
Указание. Проверив, что данный ряд равномерно сходится в интервале  , покажите, что ряд
, покажите, что ряд  расходится всюду.
расходится всюду.
Литература: [5, гл. 12].
О рядах
В «бесконечной» сумме  процесс сложения никогда не кончается, за каждым слагаемым всегда стоит следующее.
процесс сложения никогда не кончается, за каждым слагаемым всегда стоит следующее.
Ряд 
(его члены образуют геометрическую прогрессию со знаменателем x) в случае  стремится к 1/(1 -x). Поэтому пишут:
стремится к 1/(1 -x). Поэтому пишут:
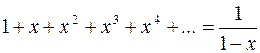 или
или 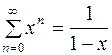 .
.
Сумма этого ряда была определена впервые в III в. до н.э. (из истории математики). Архимед применил суммирование бесконечной геометрической прогрессии со знаменателем 1/4.
После Архимеда вплоть до XVI в. рядами не занимались. С XVI в. началось изучение изменяющихся процессов. Для знакочередующегося ряда

Г. Лейбниц находит сумму. Она равна p /4.
Л. Эйлер нашел сумму для ряда  ,
,
 ,
,  .
.
Это дало возможность приближенно вычислить число π с любой степенью точности (если взять достаточно много слагаемых).
Понятие сходимости ряда в XVI в. точно установлено еще не было, и считалось, что любой ряд имеет сумму и что с рядами можно выполнять такие же арифметические действия, как и с многочленами: складывать, умножать, переставлять слагаемые и т.п. И это часто приводило к фантастическим результатам. Например, получали, что сумма ряда  могла быть и 0, и 1, и даже 1/2.
могла быть и 0, и 1, и даже 1/2.
Рассуждения были примерно следующие:
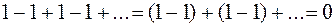 или
или
 .
.
Пусть  ; перепишем S так:
; перепишем S так:
 , т.е.
, т.е.  , откуда
, откуда  .
.
И только когда началось систематическое изучение рядов (начало XIX в.), было установлено, что, например, абсолютно сходящиеся ряды не меняют сумму при перестановке членов.
Идея представления функций степенными рядами принадлежит
И. Ньютону. Он нашел разложения многих функций.
Например,
 ,
,
где x – радианная мера угла.
Так, ряд  дает разложение функции
дает разложение функции  .
.
Если
 ,
,
то, ограничиваясь несколькими первыми членами, мы получим приближенное представление функции: оно тем точнее, чем больше будет взято членов ряда (слагаемых).
При рассмотрении периодических процессов пользуются тригонометрическими рядами:
 .
.
Формулы, по которым определяются коэффициенты  функции
функции  , – формулы Фурье – дают название таким рядам – ряды Фурье.
, – формулы Фурье – дают название таким рядам – ряды Фурье.
Числовые ряды
Определение. Выражение
 (1)
(1)
называется рядом, где  – последовательность чисел или функций. Слагаемые
– последовательность чисел или функций. Слагаемые  – это члены ряда,
– это члены ряда, 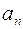 – общий член ряда.
– общий член ряда.
Ряд называется числовым, если все его члены являются числами.
Ряд является функциональным, если все члены ряда – функции.
Сумма ряда
Определение. Сумма конечного числа  первых членов ряда называется n -й частичной суммой ряда:
первых членов ряда называется n -й частичной суммой ряда:
 . (2)
. (2)
 – первая частичная сумма,
– первая частичная сумма,
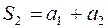 – вторая частичная сумма,
– вторая частичная сумма,
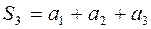 – третья частичная сумма,
– третья частичная сумма,
…………………………………………………………….
 – n -я частичная сумма и т.д.
– n -я частичная сумма и т.д.
Определение. Если существует конечный предел последовательности частичных сумм
 , (3)
, (3)
то его называют суммой ряда и говорят, что ряд сходится. Если  не существует, то говорят, что ряд расходится и суммы не имеет. При этом пишут:
не существует, то говорят, что ряд расходится и суммы не имеет. При этом пишут:  .
.
задача 1.31 [7]
Найти сумму ряда  .
.
Решение:
Общий член ряда следует упростить. Представим его суммой двух простейших дробей. Знаменатель  разложим на множители.
разложим на множители.
 , тогда
, тогда  ,
,  .
.
 .
.
 .
.
Значения коэффициентов А и В найдем устно: чтобы при сложении дробей в числителе получилось 14, надо положить А = 1, В = –1.
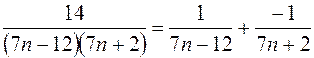 .
.
Далее найдем  (для формулы (3)).
(для формулы (3)).
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
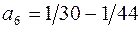 ,
,
 ,
,
………………………
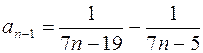 ,
,
 .
.
Чтобы вывести формулу для конечной суммы 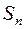 , проанализируем некоторые частичные суммы.
, проанализируем некоторые частичные суммы.
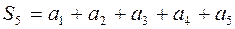
 ,
,
 ,
,
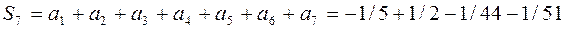 .
.
Таким образом, n -я частичная сумма
 .
.
 .
.
 .
.
Задача 2.31 [7]
Найти сумму ряда  .
.
Решение:
Как и в первой задаче, сначала упростим  . Разложим правильную рациональную дробь
. Разложим правильную рациональную дробь  на простейшие дроби. Такую операцию мы часто выполняли, например, при интегрировании рациональных дробей.
на простейшие дроби. Такую операцию мы часто выполняли, например, при интегрировании рациональных дробей.
 .
.
Выпишем столбцом a1, a2,, a3,…, an. При этом расположим слагаемые с одинаковыми знаменателями друг под другом:
 ,
,

 ,
,

 ,
,

 ,
,

 ,
,
……………………………….…
 ,
,

 ,
,

 .
.
В столбцах со знаменателями 3, 4, 5 получим соответственно:  ,
,  ,
, 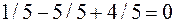 и т.д.
и т.д.
Тогда, например,  ,
,
 и т.д.
и т.д.

Сумма  , т.е.
, т.е.
 .
.
Примечание. Важнейшей задачей теории числовых рядов является вычисление их сумм. В задачах 1.31, 2.31 это можно было сделать с помощью формулы (3). Но такое нахождение суммы ряда часто требует громоздких выкладок или даже невозможно (см. задачу 3.31). Тогда пользуются различными признаками сходимости рядов. Для сходящегося ряда ограничиваются приближенным вычислением его суммы, заменяя ее частичной суммой с достаточно большим числом членов и оценивая допущенную погрешность (см. задачу 9.31).
Не нашли, что искали? Воспользуйтесь поиском: