Знакопеременные ряды

Определение 1. Числовые ряды, члены которых как положительные числа, так и отрицательные, называются знакопеременными.

Знакочередующиеся ряды

являются частным случаем рядов знакопеременных.

Определение 2. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд называется условно или неабсолютно сходящимся.

Теорема

Если сходится ряд, составленный из абсолютных величин членов данного ряда, то сходится и данный ряд, называемый в этом случае абсолютно сходящимся.

Теорема Лейбница (достаточный признак сходимости
знакочередующегося ряда)

Если абсолютные величины членов знакочередующегося ряда , монотонно убывают и абсолютная величина общего члена ряда стремится к нулю при , то ряд сходится, его сумма положительна и меньше первого члена.

Следствие. При замене суммы ряда частичной суммой мы отбрасываем все члены ряда начиная с , т.е. отбрасываем знакочередующийся ряд, который удовлетворяет признаку Лейбница. Сумма этого ряда по абсолютной величине меньше модуля первого члена ряда, т.е. меньше . Значит, абсолютная величина допущенной ошибки при такой замене на будет меньше абсолютной величины первого члена отброшенной части ряда.

Примечания:

1. Исследование сходимости знакопеременных рядов следует начинать с исследования их абсолютной сходимости, так как это часто приводит быстрее к цели, чем применение признака Лейбница с последующим выяснением абсолютной сходимости ряда.

2. Для знакоположительных рядов мы будем применять один из пяти признаков их сходимости (пп. 2.4.1 – 2.4.4).

Задача 8.31 [7]

Исследовать на сходимость ряд .

Решение:

Этот ряд знакопеременный. Исследуем его на абсолютную сходимость. Составляя ряд из абсолютных величин (модулей) членов данного ряда, получим ряд . Применим признак Даламбера. Выпишем члены и ; , .

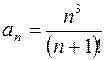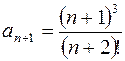Тогда ,

, т.е. ряд сходится. Следовательно, исходный ряд сходится абсолютно.

Задача 9.31 [7]

Вычислить сумму ряда с точностью .

, .

Решение:

Прежде чем искать приближенно сумму данного ряда, надо знать, что она действительно существует, т.е. что данный ряд сходится. Проверяем сходимость ряда по признаку Лейбница: его члены монотонно убывают по абсолютному значению (убедитесь в этом самостоятельно), и .

Находим первые члены ряда с четырьмя знаками 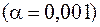после запятой (в приближенных вычислениях надо брать одну запасную цифру).

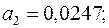
Получили: .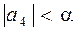

Таким образом, достаточно взять первые три члена ряда, чтобы его сумма удовлетворяла заданной точности.

.

Согласно следствию из теоремы Лейбница, допущенная ошибка вычисления суммы ряда меньше 0,001.

Задача 10.31 [7]

Доказать справедливость равенства .

Решение:

Рассмотрим ряд . Исследуем его на сходимость, применяя признак Даламбера: , .

, ряд сходится.

Тогда по необходимому признаку сходимости числового ряда следует, что его -й член стремится к нулю при , т.е. .

Не нашли, что искали? Воспользуйтесь поиском: