Равномерная сходимость функционального ряда

Для каждого значения x ₀ из области сходимости ряда , т.е. остаток сходящегося ряда стремится к нулю при .

Определение. Функциональный ряд называется равномерно сходящимся в некотором интервале, если он сходится для всех x из этого интервала и если для всякого числа e > 0 существует такое число N > 0, зависящее от e и не зависящее от x. (при n > N выполняется неравенство для всех x из рассматриваемого интервала).

Задача 15.31 [7]

Доказать, исходя из определения, равномерную сходимость функционального ряда на отрезке [0, 1]. При каких n абсолютная величина остаточного члена ряда не превосходит 0,1 для всех ?

Решение:

Найдем область абсолютной сходимости данного ряда, т.е. область сходимости ряда , пользуясь признаком Даламбера.

, ;

, т.е. m = | x |.

Данный ряд сходится для всех значений x при , т.е. , .

При x= 1 получается ряд – числовой знакочередующийся, который сходится по признаку Лейбница (проверьте это самостоятельно).

Итак, ряд сходится на отрезке . Теперь нужно убедиться, что для любого можно подобрать такой номер , что при всяком будет иметь место неравенство для всех .

.

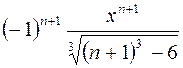– первый член этого ряда.

Тогда (следствие теоремы Лейбница: сумма знакочередующегося ряда не превосходит первый член ряда).

На отрезке выражение принимает наибольшее значение при . Тогда для всех этого отрезка.

Пусть – любое фиксированное число. Выясним, при каких для всех 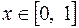справедливо неравенство . Оно будет выполняться при .

Решим это неравенство: , .

Примем за номер 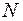целую часть . Итак, при для всех 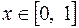. Равномерная сходимость ряда установлена.

Вычислим при ; .

Итак, при абсолютная величина остаточного члена ряда не превосходит 0,1 для всех .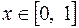

Не нашли, что искали? Воспользуйтесь поиском: