Достаточные признаки сходимости рядов

С положительными членами

Признак сравнения

Теорема (непредельная форма признака сравнения)

Пусть даны два положительных ряда:

, ,

, .

Если члены первого ряда не больше соответствующих членов второго ряда и второй ряд сходится, то первый ряд тоже сходится.

Итак, если и , то .

Теорема

Если члены первого ряда не меньше соответствующих членов второго ряда и второй ряд расходится, то первый ряд тоже расходится.

Примечания:

1. Эти две теоремы представляют первый признак сравнения.

2. Часто оказывается полезным рассматривать не соотношение между общими членами a_n, b_n рядов, а предел их отношения при , то есть предельную форму первого признака сравнения.

Теорема (второй признак сравнения)

Если для знакоположительных рядов

,

, (4)

то эти ряды одновременно сходятся или расходятся.

Следствие. Теорема имеет место, если .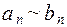

Признак Даламбера

Теорема (предельная форма признака)

Если для знакоположительного ряда существует

, (5)

то при ряд сходится, при ряд расходится; при вопрос о сходимости ряда остается открытым (в этом случае необходимо применять другие признаки сходимости рядов).

Признак Коши

Теорема (предельная форма признака)

Если существует

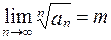, (6)

то при ряд , , сходится; при – расходится, при ряд может сходиться или расходиться (требуется дополнительное исследование).

Не нашли, что искали? Воспользуйтесь поиском: