
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Интегрирование и дифференцирование степенных рядов
Определение. Функциональный ряд вида
 ,
,
где 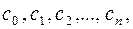 … – действительные числа, называется степенным рядом.
… – действительные числа, называется степенным рядом.
Областью абсолютной сходимости ряда является интервал  , где число R – радиус сходимости.
, где число R – радиус сходимости.
Пусть степенной ряд  имеет радиус сходимости R > 0. Тогда справедливы следующие положения:
имеет радиус сходимости R > 0. Тогда справедливы следующие положения:
1. Сумма ряда является непрерывной функцией от x во всем интервале сходимости  .
.
2. Ряд равномерно сходится на любом отрезке  , где
, где  .
.
3. Ряд можно почленно интегрировать по любому отрезку  , лежащему внутри интервала
, лежащему внутри интервала  .
.
4. Ряд можно почленно дифференцировать в любой точке  сколь угодно раз.
сколь угодно раз.
Примечания:
1. При почленном интегрировании или дифференцировании степенного ряда получаются новые степенные ряды, при этом их радиус сходимости остается тот же.
2. Радиус сходимости степенного ряда можно найти по одной из формул:
 , (10)
, (10)
 (11)
(11)
при условии, что указанные пределы существуют, 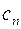 – коэффициент ряда.
– коэффициент ряда.
Задача 17.31 [7]
Найти сумму ряда  .
.
Решение:
I способ. Найдем интервал сходимости ряда:
 ,
,  ,
,  .
.
Упростим рациональную дробь  ,
,  .
.
Тогда ряд может быть представлен разностью двух рядов:
 .
.
Сходимость каждого из них остается та же  (убедитесь в этом самостоятельно). Поэтому равенство имеет место. Обозначим суммы рядов соответственно
(убедитесь в этом самостоятельно). Поэтому равенство имеет место. Обозначим суммы рядов соответственно  и
и  , а искомую сумму – через
, а искомую сумму – через  ,
,  .
.
Найдем сумму первого ряда:
 .
.
Дифференцируя почленно ряд внутри интервала сходимости  , получим:
, получим:  ;
; 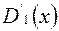 представляет собой геометрическую прогрессию со знаменателем
представляет собой геометрическую прогрессию со знаменателем  .
.
При  прогрессия сходится,
прогрессия сходится,  ,
,  ,
,  и сумма равна:
и сумма равна: 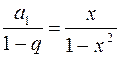 ;
;  . Теперь, интегрируя
. Теперь, интегрируя 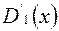 на отрезке
на отрезке  , лежащем внутри интервала сходимости
, лежащем внутри интервала сходимости  , получим:
, получим:
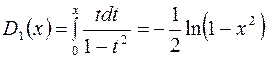 .
.
Найдем сумму  второго ряда:
второго ряда:
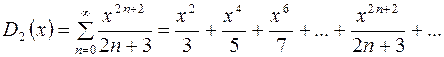 .
.
Выполним преобразование:
 .
.
Обозначим сумму ряда, стоящего в скобках, через  и продифференцируем
и продифференцируем  в интервале
в интервале  :
:
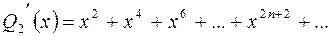 – это тоже геометрическая прогрессия.
– это тоже геометрическая прогрессия.
 ,
,  ,
, 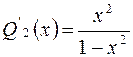 ;
;

 .
.
Итак, сумма исходного ряда равна:

 или
или 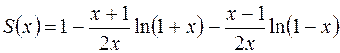
для  .
.
II способ. Не повторяя подробностей I способа, связанных с интервалом сходимости данного ряда, предлагаем II вариант решения задачи. Обозначим сумму ряда через  :
:  .
.
Умножим на  данный ряд:
данный ряд: 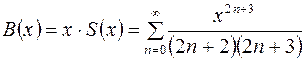 . Продифференцируем дважды полученный ряд:
. Продифференцируем дважды полученный ряд:
 ,
,
 .
.
 представляет собой геометрическую прогрессию со знаменателем
представляет собой геометрическую прогрессию со знаменателем 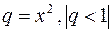 , тогда
, тогда  . Проинтегрируем
. Проинтегрируем  на отрезке
на отрезке  :
:
 .
.
Интегрируя  по частям, получим:
по частям, получим:


для  .
.
Задача 18.31 [7]
Найти сумму ряда  .
.
Решение:
Данный ряд сходится в интервале  (убедитесь в этом самостоятельно). Перепишем его, представив в виде суммы трех рядов:
(убедитесь в этом самостоятельно). Перепишем его, представив в виде суммы трех рядов:
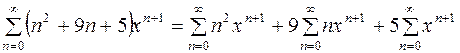 .
.
Это возможно, так как каждый из рядов имеет одну и ту же область сходимости – интервал  . Обозначим суммы трех рядов соответственно через
. Обозначим суммы трех рядов соответственно через 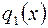 ,
,  ,
,  , а искомую сумму – через
, а искомую сумму – через  .
.
 .
.
 ,
,
как сумма членов геометрической прогрессии со знаменателем 
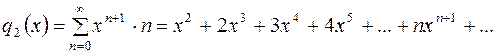 .
.
Выполним преобразование:
 .
.
Обозначим через  сумму ряда
сумму ряда  .
.
Интегрируя почленно этот ряд на отрезке  внутри интервала сходимости
внутри интервала сходимости  , получим:
, получим:
 .
.
Чтобы найти  , надо продифференцировать дробь
, надо продифференцировать дробь  :
:
 .
.
Следовательно, 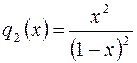 .
.
Теперь найдем 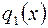 :
:
 .
.
Вынесем  за скобки:
за скобки:
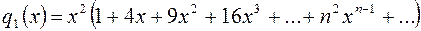 .
.
Обозначим через 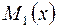 сумму ряда, стоящего в скобках. Тогда
сумму ряда, стоящего в скобках. Тогда 
В этих скобках стоит ряд, сумма которого найдена: 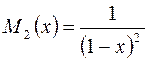 . Получаем:
. Получаем: 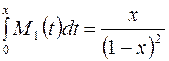 .
.
Отсюда  .
.
Но  ,
, 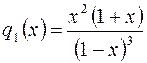 . Тогда сумма исходного ряда
. Тогда сумма исходного ряда
 .
.
Итак, 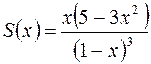 для
для  .
.
Ряд Тейлора
Определение. Ряд 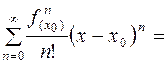

называется рядом Тейлора по степеням  для функции
для функции 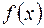 .
.
Функция 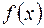 может быть разложена в ряд Тейлора, если в рассматриваемой точке
может быть разложена в ряд Тейлора, если в рассматриваемой точке  она имеет производные всех порядков и если остаточный член в точке
она имеет производные всех порядков и если остаточный член в точке  при
при  стремится к нулю. При
стремится к нулю. При  ряд Тейлора называют иногда рядом Маклорена.
ряд Тейлора называют иногда рядом Маклорена.
Теорема
Если функция разлагается в степенной ряд, то для неё этот ряд единственный и является рядом Тейлора.
Примечание. Находя последовательно производные функции 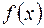 и их значения в точке
и их значения в точке  , можно записать ряд Тейлора. Но при этом исследование остаточного члена
, можно записать ряд Тейлора. Но при этом исследование остаточного члена  представляет большие трудности. Поэтому часто идут другим путем: пользуются готовыми разложениями основных элементарных функций в степенные ряды в комбинациях с правилами сложения, вычитания, умножения рядов и теоремами об их интегрировании и дифференцировании, как это, например, было показано в задачах 17.31 и 18.31.
представляет большие трудности. Поэтому часто идут другим путем: пользуются готовыми разложениями основных элементарных функций в степенные ряды в комбинациях с правилами сложения, вычитания, умножения рядов и теоремами об их интегрировании и дифференцировании, как это, например, было показано в задачах 17.31 и 18.31.
Задача 19.31 [7]
Разложить функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням  .
.
Решение:
х 0 = 0. Воспользуемся примечанием. Так как
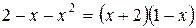 ,
,
то функция упрощается, если применить метод неопределенных коэффициентов:
 .
.
Далее раскладываем в ряд каждое слагаемое, пользуясь геометрической прогрессией:
 .
.
Сумма членов геометрической прогрессии со знаменателем  равна:
равна:  . В нашем случае
. В нашем случае  .
. 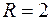 – радиус сходимости этого ряда. Слагаемое
– радиус сходимости этого ряда. Слагаемое  ,
, 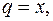

Складывая ряды, получим:  или
или 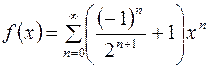 , где
, где  – общая область сходимости.
– общая область сходимости.
4.1 Приближенное вычисление интегралов с помощью
степенных рядов
Чтобы вычислить интеграл 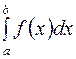 с заданной точностью, подынтегральную функцию
с заданной точностью, подынтегральную функцию 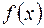 раскладывают в ряд, производят интегрирование и в полученном ряде оставляют столько членов, сколько потребуется для заданной точности (см. задачу 9.31).
раскладывают в ряд, производят интегрирование и в полученном ряде оставляют столько членов, сколько потребуется для заданной точности (см. задачу 9.31).
Задача 20.31 [7]
Вычислить интеграл  с точностью до 0,001.
с точностью до 0,001.
Решение:
Пользуясь разложением функции  в ряд Маклорена, заменяя в нем
в ряд Маклорена, заменяя в нем  на
на  , имеем:
, имеем:
 .
.
Toгдa

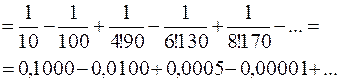
Почленное интегрирование законно, так как отрезок интегрирования  целиком лежит в области сходимости ряда
целиком лежит в области сходимости ряда  .
.
Чтобы вычислить данный интеграл с точностью до 0,001, надо взять в полученном ряде два его члена (0,0005<0,001) (см. задачу 9.31).
Таким образом,
 .
.
Вопросы для самопроверки
Числовые ряды
1. Дайте определения сходящихся и расходящихся рядов.
2. Сформулируйте необходимый признак сходимости ряда.
3. Сформулируйте достаточные признаки сходимости рядов с положительными членами: сравнение рядов с положительными членами; признак Даламбера; радикальный признак Коши, интегральный признак Коши.
4. Дайте определение абсолютно сходящегося ряда. Сформулируйте свойства абсолютно сходящихся рядов.
5. Сформулируйте признак Лейбница.
Не нашли, что искали? Воспользуйтесь поиском: