Признак Вейерштрасса

Для установления равномерной сходимости функционального ряда на отрезке служат и достаточные признаки равно­мерной сходимости. Рассмотрим один из них.

Теорема (признак Вейерштрасса)

Если существует сходящийся числовой ряд с положительными членами 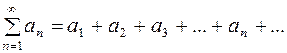и при этом выполняются соотношения: для всех , в котором определены члены функционального ряда 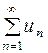, то этот ряд сходится равномерно (и абсолютно) в интервале .

В этом случае ряд , члены которого превосходят абсолютные величины соответствующих членов ряда 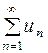, называется мажорантным рядом для .

Примечание. Если сходится ряд , то можно найти такое положительное целое число 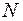(номер), не зависящее от , что при 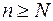модуль будет меньше любого наперед заданного положительного числа .

Задача 16.31 [7]

Для данного функционального ряда построить мажорирующий ряд и доказать равномерную сходимость на указанном отрезке: , .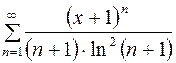

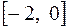Решение:

Воспользуемся признаком Вейерштрасса. Отрезок 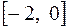входит в область определения членов данного функционального ряда (члены ряда определены на всей числовой оси). Для всех 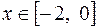имеет место неравенство:

.

Пользуясь интегральным признаком сходимости, покажем, что числовой ряд с положительными членами 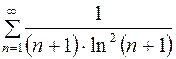сходится.

Рассмотрим функцию . Она непрерывна, монотонно убывает и положительна для значений 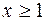. Поэтому можно применить указанный признак.

Несобственный интеграл

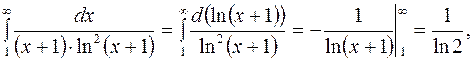т.е. сходится. Следовательно, ряд 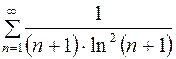сходится. Значит, ряд 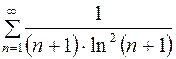является мажорантным для данного функционального ряда.

Таким образом, все условия признака Вейерштрасса выполнены, поэтому заданный ряд сходится равномерно (и абсолютно) на указанном отрезке.

Не нашли, что искали? Воспользуйтесь поиском: