Функциональные ряды

Рассмотрим ряд

, (7)

где все функции определены в одном и том же промежутке, называемом областью определения ряда. Придавая аргументу определенные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися.

Совокупность тех значений х, при которых функциональный ряд сходится, называется областью его сходимости.

В области сходимости сумма функционального ряда является некоторой функцией от х:

, (8)

где , х принадлежит области сходимости ряда (7).

Разность (9)

называется n -м остатком ряда.

Так как исследование сходимости функциональных рядов сводится к исследованию сходимости числовых рядов, то для нахождения областей сходимости функциональных рядов можно применять достаточные признаки сходимости числовых рядов. При этом различают области абсолютной и условной сходимости функционального ряда.

Задача 11.31 [7]

Найти область сходимости функционального ряда .

Решение:

Рассмотрим ряд . Сравним его с числовым рядом 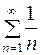, используя второй признак сравнения (п. 2.4.1). Найдем предел частного общих членов этих рядов при :

.

Следовательно, ряд расходится, так как расходится гармонический ряд. Далее воспользуемся теоремой: если ряд расходится и 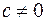(с – какое-либо фиксированное число), то ряд также расходится. В данном случае 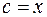, 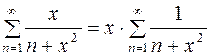. Значит, при ряд расходится. При 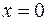все члены функционального ряда равны нулю, при 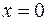, т.е. ряд сходится. Итак, данный ряд расходится при всех х, кроме .

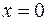Задача 12.31 [7]

Найти область сходимости функционального ряда .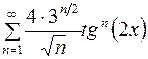

Решение:

Применим признак Даламбера:

, ;

Данный ряд будет сходиться, причем абсолютно, для тех значений , при которых .

Решим полученное неравенство:

;

, , .

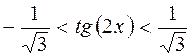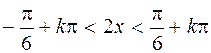При . Исследуем сходимость данного ряда в этих точках.

При получаем ряд .

Ряд Дирихле расходится при (см. задачу 3.31). При получим знакочередующий ряд . По признаку Лейбница он сходится, но не абсолютно.

Таким образом, данный ряд сходится при , .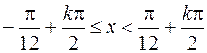

Задача 13.31 [7]

Найти область сходимости функционального ряда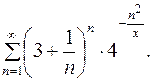

Решение:

Члены данного ряда определены на всей числовой оси, за исключением 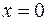. Эта точка не принадлежит области определения ряда. Исследуем ряд на сходимость с помощью радикального признака Коши.

.

Найдем .

при всех допустимых значениях х. Итак, данный ряд сходится при всех х, кроме х = 0.

Задача 14.31 [7]

Найти область сходимости функционального ряда .

Решение:

Воспользуемся признаком Даламбера:

, ;

.

При m < 1 данный ряд будет сходиться, т.е. x ² < 1, | x | < 1,

–1 < x < 1.

Исследуем границы интервала . При получим ряд , который расходится, так как
(см. п. 2.3). Следовательно, областью сходимости данного ряда является интервал .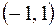

Не нашли, что искали? Воспользуйтесь поиском: