Интегральный признак Коши

Теорема

Если функция 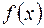непрерывная, положительная, не возрастающая для 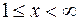и при натуральных значениях аргумента x

, ,..., ,...,

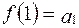то ряд и несобственный интеграл одновременно сходятся или расходятся.

Задача 3.31 [7]

Исследовать на сходимость ряд .

Здесь, как и в других задачах типового расчета, формулой (3) не пользуются (см. примечание к задаче 2.31).

Решение:

Так как для любого n , то для .

Исследуем на сходимость ряд с общим членом . Возьмем ряд с общим членом ; – обобщенный гармонический ряд, его также называют рядом Дирихле, он сходится при и расходится при . В данном случае , т. е. расходится.

Применим второй признак сравнения. Найдем

.

Следовательно, оба ряда ведут себя одинаково в смысле сходимости.

Так как ряд Дирихле расходится, то ряд также расходится. Возвращаясь к соотношению , по первому признаку сравнения заключаем: данный ряд расходится.

задача 4.31 [7]

Исследовать на сходимость ряд .

Решение:

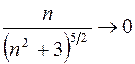Воспользуемся эквивалентным равенством: при , при . Поэтому . Значит, рассматриваем ряд . Сравним его со сходящимся рядом Дирихле . Найдем p по теореме (второй признак сравнения):

, ,

то есть ряд сходится. Следовательно, сходится и данный ряд.

Примечание. Решение задачи намного упрощается с помощью следствия второго признака сравнения (см. п. 2.4.1). Проверьте это самостоятельно.

задача 5.31 [7]

Исследовать на сходимость ряд .

Решение:

Найдем , применив признак Даламбера.

В данном случае ,

;

Таким образом, , данный ряд расходится.

задача 6.31 [7]

Исследовать на сходимость ряд .

Решение:

Здесь . Воспользуемся радикальным признаком Коши: =

.

Так как , то данный ряд сходится.

Задача 7.31 [7]

Исследовать на сходимость ряд .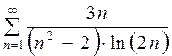

Решение:

Рассмотрим вспомогательный ряд с общим членом : (знак ~ понимаетсякак эквивалентность числовых последовательностей и при ), .

Исследуем его на сходимость, пользуясь интегральным признаком Коши.

В данном случае функция удовлетворяет условиям интегрального признака при (убедитесь в этом самостоятельно).

Несобственный интеграл

, т.е. расходится, поэтому расходится и ряд. Тогда по следствию из теоремы (второй признак сравнения) заключаем, что заданный ряд тоже расходится.

Не нашли, что искали? Воспользуйтесь поиском: