
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Непосредственный подсчет вероятностей в рамках классической схемы
Математика
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Рекомендовано ФГБОУ ВПО «Госуниверситет-УНПК»
для использования в учебном процессе в качестве учебного пособия
для высшего профессионального образования
Орел 2014
УДК 519.2 (075)
ББК 22.17я7
З-17
Рецензенты:
доктор технических наук, профессор, заведующий кафедрой «Высшая математика»
Федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Государственный университет – учебно-научно-производственный комплекс»
В.А. Гордон,
кандидат педагогических наук, доцент кафедры «Математика»
Федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Орловский государственный аграрный университет»
Е.В. Александрова
Заика, А.В.
З-17 Математика. Теория вероятностей: учебное пособие для высшего профессионального образования / А.В. Заика, О.В. Кирсанова. – Орел: ФГБОУ ВПО «Госуниверситет-УНПК», 2014. – 89 с.
Учебное пособие содержит теоретический материал и индивидуальные задания (30 вариантов) по теории вероятностей для самостоятельной работы.
Предназначено студентам всех специальностей очной формы обучения, изучающим дисциплину «Математика».
УДК 519.2 (075)
ББК 22.17я7
| © ФГБОУ ВПО «Госуниверситет-УНПК», 2014 |
СОДЕРЖАНИЕ
| Предисловие_______________________________________ | |
| Введение__________________________________________ | |
| 1. СЛУЧАЙНЫЕ СОБЫТИЯ | |
| 1.1. Основные понятия____________________________________ | |
| 1.2. Непосредственный подсчет вероятностей в рамках классической схемы_______________________________________ | |
| 1.3. Геометрическое определение вероятности_____________ | |
| 1.4. Теоремы сложения и умножения вероятностей________ | |
| 1.5. Формула полной вероятности и формула Байеса_______ | |
| 1.6. Повторение опытов (схема Бернулли)________________ | |
| 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ | |
| 2.1. Дискретные случайные величины___________________ | |
| 2.2. Непрерывные случайные величины__________________ | |
| 3. РАСЧЕТНЫЕ ЗАДАНИЯ | |
| Задание 1___________________________________________ | |
| Задание 2___________________________________________ | |
| Задание 3___________________________________________ | |
| Задание 4___________________________________________ | |
| Задание 5___________________________________________ | |
| Задание 6___________________________________________ | |
| Задание 7___________________________________________ | |
| Задание 8___________________________________________ | |
| Задание 9___________________________________________ | |
| Задание 10__________________________________________ | |
| Задание 11__________________________________________ | |
| Задание 12__________________________________________ | |
| Задание 13__________________________________________ | |
| Задание 14__________________________________________ | |
| Задание 15__________________________________________ | |
| Задание 16__________________________________________ | |
| Задание 17__________________________________________ | |
| ЛИТЕРАТУРА ___________________________________________ | |
| ПРИЛОЖЕНИЯ ___________________________________________ |
ПРЕДИСЛОВИЕ
Теория вероятностей, согласно действующим государственным образовательным стандартам, входит в рабочие программы по мате-матике целого ряда специальностей. Учебное пособие предназначено для студентов дневного и вечернего очного отделения.
Предлагаемое пособие имеет следующую структуру. В первой части приводится краткое изложение теории. Многие определения, теоремы и формулы сопровождаются замечаниями и комментариями, которые позволяют раскрыть содержание вводимых понятий, смысл теорем и формул.
Активная самостоятельная работа студентов – залог успешного освоения материала. Одной из форм активизации учебного процесса по математике служит система типовых расчетов. Во второю часть настоящего пособия включены расчетные задания, которые предста-влены 30-ю вариантами каждое, что позволяет предложить индиви-дуальные задания всем студентам группы.
Расчетные задания пособия охватывают следующие разделы теории вероятностей: случайные события (классическое определение вероятности, геометрическое определение вероятности, теоремы сло-жения и умножения вероятностей, формула полной вероятности, фор-мула Байеса, схема Бернулли) и случайные величины (дискретные и непрерывные, их распределения).
При выполнении типового расчета необходимо строго придер-живаться указанных ниже правил. Работы, выполненные без соблю-дения этих правил, не засчитываются и возвращаются студенту для переработки.
Расчетные задания решаются студентами самостоятельно и сдаются на проверку в указанные преподавателем сроки. На титульном листе типового расчета должны быть ясно написаны следующие сведения: наименование учебного заведения, факультета, учебной дисциплины, фамилия и инициалы, номера группы и варианта студента, выполняющего данную работу, а также дата сдачи. Решение каждой задачи приводится на отдельном листе стандартного формата с указыванием на нем: номера задания, фамилии, инициалов, номера группы и варианта студента. В работу должны быть включены задачи строго по указанному варианту. Каждая задача должна начинаться с точной формулировки задачи и оканчиваться найденными результатами решения. Решения задач следует излагать подробно и аккуратно, объясняя все действия и делая необходимые чертежи. Неверно решенные задачи возвра-щаются на доработку с указанием характера ошибки.
ВВЕДЕНИЕ
Теория вероятностей – это математическая наука, изучающая закономерности, присущие массовым случайным явлениям. При этом изучаемые явления рассматриваются в абстрактной форме, неза-висимо от их конкретной природы. Предметом теории вероятностей являются математические модели случайных явлений.
Цель теории вероятностей – осуществление прогноза в области случайных явлений, влияние на ход и контроль этих явлений, огра-ничение сферы действия случайности.
СЛУЧАЙНЫЕ СОБЫТИЯ
Основные понятия
Случайным событием (или просто событием) называется любой исход опыта, который может произойти или не произойти.
События принято обозначать заглавными латинскими буквами А, В, С, ….
Событие называется достоверным, если оно обязательно насту-пит в результате данного опыта.
Событие называется невозможным, если оно заведомо не произойдет в результате проведения опыта.
Два события называются несовместимыми, если появление одного из них исключает появление другого события в одном и том же опыте, то есть не смогут произойти вместе в одном опыте.
В противном случае события называются совместимыми.
События А 1, А 2, …, Аn называются попарно несовместимыми, если любые два из них несовместимы.
Несколько событий образуют полную группу, если они попарно несовместимы и в результате каждого опыта происходит одно и только одно из них.
Несколько событий в данном опыте называются равновозмож-ными, если ни одно из них не является объективно более возможным, чем другие, то есть все события имеют равные шансы.
Объединением или суммой событий А и В называется событие 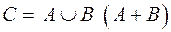 , состоящее в наступлении хотя бы одного из них (или А, или В, или А и В вместе).
, состоящее в наступлении хотя бы одного из них (или А, или В, или А и В вместе).
Пересечением или произведением событий А и В называется событие  , состоящее в совместном наступлении этих событий (т.е. А и В одновременно).
, состоящее в совместном наступлении этих событий (т.е. А и В одновременно).
Противоположным событию А является событие  , которое происходит тогда и только тогда, когда не происходит событие А (т.е.
, которое происходит тогда и только тогда, когда не происходит событие А (т.е.  – событие А не наступает).
– событие А не наступает).
Непосредственный подсчет вероятностей в рамках классической схемы
Классическая схема охватывает те опыты, элементарные исходы которых удовлетворяют следующим условиям:
1) элементарные исходы образуют конечное множество n элементов;
2) элементарные исходы образуют полную группу попарно несовместимых исходов;
3) элементарные исходы равновозможны.
Тогда  ,
,
где m – число элементарных исходов, благоприятствующих событию А, то есть элементарных исходов, при которых событие А происходит;
n – число всех исходов.
При подсчете числа исходов часто используют формулы комбинаторики. Комбинаторика связана с подсчетом числа комби-наций, которые можно составить из данных элементов, соблюдая те или иные условия.
Размещения – это выборки (комбинации), состоящие из m элементов, которые отличаются друг от друга либо составом элементов, либо порядком их расположения. Число размещений из n различных элементов по m элементов обозначается символом  и вычисляется по формуле
и вычисляется по формуле
 .
.
Если среди элементов множества имеются одинаковые элемен-ты, то размещения называются размещениями с повторениями. Число размещений из n элементов по m элементов с повторениями обозна-чается символом 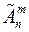 и вычисляется по формуле
и вычисляется по формуле
 .
.
Перестановки – это выборки (комбинации), состоящие из n элементов и отличающиеся друг от друга только порядком следо-вания элементов. Число перестановок из n различных элементов обозначается символом  и вычисляется по формуле
и вычисляется по формуле
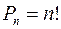 .
.
Число перестановок с повторениями из n элементов обозна-чается символом 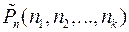 и вычисляется по формуле
и вычисляется по формуле
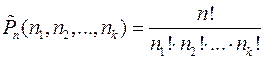 ,
,
где  – число повторов первого элемента множества;
– число повторов первого элемента множества;
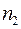 – число повторов второго элемента множества;
– число повторов второго элемента множества;
 ;
;
 – число повторов k -го элемента множества, причем
– число повторов k -го элемента множества, причем
 .
.
Сочетания – это выборки (комбинации), которые отличаются друг от друга только составом элементов. Число сочетаний из n различных элементов по m элементов обозначается символом  и вычисляется по формуле
и вычисляется по формуле
 .
.
Число сочетаний с повторениями из n элементов по m элементов обозначается символом 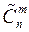 и вычисляется по формуле
и вычисляется по формуле
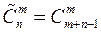 .
.
Правило умножения: если из некоторого конечного множества объект х можно выбрать n 1 способами и после каждого такого выбора объект у можно выбрать n 2 cпособами, то оба объекта х и у, в указанном порядке можно выбрать n 1· n 2 способами.
Правило сложения: Если некотрый объект х можно выбрать n 1 способами, а объект у можно выбрать n 2 способами, то любой из указанных объектов х или у можно выбрать n 1 + n 2 способами.
Замечание: эти правила распространяются на любое конечное число объектов.
Не нашли, что искали? Воспользуйтесь поиском: