Повторение опытов (схема Бернулли)

Опишем схему Бернули: пусть производятся n независимых опытов (испытаний), в каждом из которых событие А может нас-тупить с вероятностью p (обычно появление А называют успехом). Обозначим через 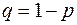вероятность того, что событие А не насту-пит (неудача).

Задача, в которой находят вероятность 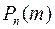наступления события А в n испытаниях ровно m раз, называется локальной.

Задача, в которой находят вероятность наступле-ния события А в n испытаниях в границах от m ₁ до m ₂ раз вклю-чительно, называется интегральной.

Для любого m = 0, 1,…, n справедлива формула Бернулли:

, где .

С помощью формулы Бернулли можно решать и интегральную задачу:

.

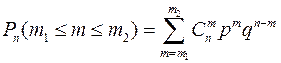Значение m = m ₀, при котором вероятность принимает наиболь-шее значение, называется наивероятнейшим числом успехов и нахо-дится из условий:

где 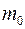– целое.

Использование формулы Бернулли при больших значениях n и m вызывает большие трудности, так как это связано с громоздкими вычислениями.

Рассмотрим асимптотические формулы Пуассона и Муавра – Лапласа, которые при достаточно больших n позволяют приближенно найт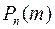и и .

Если число испытаний n – велико, а вероятность наступления события А в каждом испытании p – мала, то используют формулу Пуассона.

, где .

Вероятность того, что число успехов по схеме Бернулли заключено в пределах от m ₁ до m ₂ включительно вычисляется по формуле:

.

В тех случаях, когда число испытаний n велико, а вероятность p не близка к нулю, для вычисления вероятности 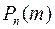используют локальную формулу Муавра – Лапласа:

, где , .

Для функции φ (x) составлены таблицы значений (табл. 1 в при-ложении А). Пользуясь табл. 1, следует учитывать, что:

1. функция φ (x) – четная, т.е. φ (- x) = φ (x);

2. при x ≥ 4 можно считать, что φ (x) = 0.

Вероятность того, что число успехов заключено в пределах от m ₁ до m ₂ включительно, вычисляется по интегральной формуле Муавра – Лапласа:

,

где , , .

Для функции 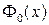составлены таблицы значений (табл. 2 в при-ложении Б

). Пользуясь табл. 2, следует учитывать, что:

1) функция 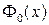– нечетная, т.е. ;

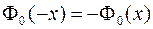2) при x ≥ 5 можно считать, что = 0,5.

Замечание. Данная приближенная формула остается в силе и в том случае, когда входящие в нее неравенства являются строгими.

Замечание. На практике выбор между формулами Муавра – Лапласа и Пуассона осуществляется по следующему критерию: если np ≤ 10, то используют формулу Пуассона, в противном случае – формулы Муавра – Лапласа.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайной называют величину, которая в результате испытаний примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Не нашли, что искали? Воспользуйтесь поиском: