Теоремы сложения и умножения вероятностей

В случае, когда событие можно представить в виде линейной комбинации элементарных (более простых) событий, возникает необходимость в следующих теоремах.

Теорема сложения вероятностей совместных событий: Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления:

.

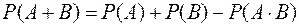При решении задач иногда удобно найти вероятность про-тивоположного события , а затем найти вероятность события 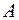по формуле

.

Для несовместных событий теорема сложения вероятностей принимает вид:

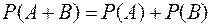
События А и В называются независимыми, если появление од-ного из них не меняет вероятность появления другого. В противном случае события называются зависимыми.

Теорема умножения вероятностей зависимых событий: Вероятность совместного наступления двух событий равна вероят-ности одного из них, умноженной на условную вероятность другого, при условии, что первое событие наступило:

.

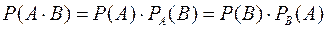Для независимых событий теорема умножения вероятностей принимает вид:

.

Замечание. Сформулированные выше теоремы могут быть распространены на любое количество сомножителей.

Не нашли, что искали? Воспользуйтесь поиском: