Примеры дискретных распределений

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

1. Биномиальное распределение. Биномиальным называют закон распределения дискретной случайной величины Х — числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события равна р; вероятности возможных значений Х = 0, 1, 2,..., т,..., п вычисляются по формуле Бернулли:

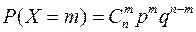Также этот закон можно задать в виде ряда распределения (табл.2).

Таблица 2. Ряд распределения дискретной случайной величины, распределенной по биномиальному закону

X			…	m	…	n
P	qⁿ	npqⁿ ^-1	…		…	pⁿ

Числовые характеристики биномиального распределения могут быть найдены по формулам:

М (Х) = np, D(X) = npq, .

2. Распределение Пуассона. Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то вместо формулыБернулли пользуются приближенной формулой Пуассона. Придавая т целые неотрицательные значения т = 0, 1, 2,..., п, можно записать ряд распределения вероятностей, вычисленных по формуле Пуассона, который называется законом распределения Пуассона:

Также этот закон можно задать в виде ряда распределения (табл.3).

Таблица 3. Ряд распределения дискретной случайной величины, распределенной по закону Пуассона

X			…	m	…	n
P			…		…

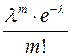
Распределение Пуассона часто используется, когда мы имеем дело с числом событий, появляющихся в промежутке времени или пространства.

Если распределение Пуассона применяется вместо биномиаль-ного, то п должно иметь порядок не менее нескольких десятков, а еще лучше нескольких сотен, а пр 10.

Числовые характеристики распределения Пуассона могут быть найдены по формулам:

М (Х) = D (X) = l, .

3. Геометрическое распределение. Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р. Испытания заканчиваются; как только появляется событие А. Таким образом, если событие А появилось в k -м испытании, то в предшествующих (k - 1) испытаниях оно не появлялось.

Дискретная случайная величина Х: {число испытаний, которые нужно провести до первого появления события А } имеет геометрическое распределение.

Свои возможные значения: 1, 2, 3, … n, … эта случайная величина принимает с вероятностями:

, где m =1, 2, 3, …, n, ….

Также этот закон можно задать в виде ряда распределения (табл.4).

Таблица 4. Ряд распределения дискретной случайной величины, распределенной по геометрическому закону

X … n …

P p pq pq ² … pqⁿ ^-¹ …

Числовые характеристики геометрического распределения мо-гут быть найдены по формулам:

, , .

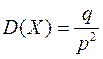Замечание. В некоторых задачах число испытаний ограничено некоторым числом k (например, запас патронов). В этом случае последняя вероятность равна

,

а числовые характеристики могут быть найдены по общим формулам.

4. Гипергеометрическое распределение. Пусть имеется множество N элементов, из которых М элементов обладают некоторым признаком А. Случайным образом без возвращения извлекаются п элементов.

Дискретная случайная величина Х: число m элементов, обладающих признаком А, среди n отобранных.

Возможные значения Х: 0, 1, 2, …, min(M, n), ес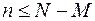ли ,

, …, min(M, n), если ;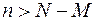

а их вероятности могут быть найдены по формуле

.

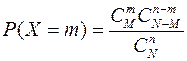Также этот закон можно задать в виде ряда распределения (табл.5).

Такой закон распределения называется гипергеометрическим.

Таблица 5. Ряд распределения дискретной случайной величины, распределенной по гипергеометрическому закону

X … n

P …

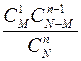
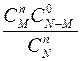
Математическое ожидание и дисперсия случайной величины т, распределенной по гипергеометрическому закону, определяются формулами:

, , .

Замечание. В случае если первые возможные значения или последние: …, n – 1, n противоречат смыслу задачи, то из ряда распределения их следует исключить, а числовые характеристики в этом случае находить по общим формулам.

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: