Непрерывные случайные величины

Непрерывной называют такую случайную величину Х, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно, а ее функция распределения непрерывна в любой точке.

Важнейшей характеристикой непрерывной случайной величины (помимо функции распределения) является плотность распределения вероятностей.

Плотностью распределения вероятностей (дифференциальной функцией распределения) непрерывной случайной величины Х называется производная ее функции распределения. Обозначается плотность распределения вероятностей через p (x) и находится по формуле

.

Плотность распределения вероятностей обладает следующими свойствами:

1) p (x) ≥ 0.

2) .

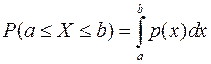3) .

4) .

График функции у = p (x) называется кривой распределения, или графиком плотности распределения. Кривая у = p (x) располагается над осью абсцисс.

Вероятность того, что в результате испытания непрерывная случайная величина X примет значение из промежутка от a до b, равна:

Также как и для дискретных случайных величин, для непрерывных случайных величин можно найти числовые характеристики.

Математическое ожидание непрерывной случайной величины Х вычисляется по формуле

.

Дисперсия непрерывной случайной величины Х вычисляется по формулам:

;

.

Среднее квадратичное отклонение непрерывной случайной величины Х вычисляется по формуле

.

Замечание. Если все возможные значения непрерывной случайной величины принадлежат интервалу 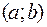, то

;

;

.

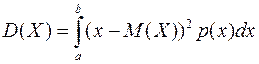Не нашли, что искали? Воспользуйтесь поиском: