Некоторые стандартные распределения непрерывных случайных величин 1 страница

1. Равномерное распределение. Непрерывная случайная величина распределена равномерно на отрезке [ a; b ], если плотность ее распределения постоянна на этом отрезке и равна нулю вне его:

Функция распределения для равномерного распределения имеет вид:

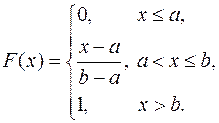
На рисунках 1 и 2 представлены графики плотности и функции распределения равномерного распределения.

Рис. 1. График плотности равномерного распределения

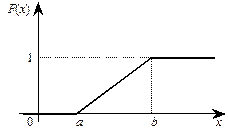Рис. 2. График функции распределения равномерного распределения

Числовые характеристики:

.

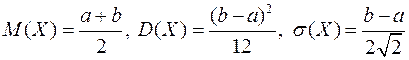Вероятность попадания непрерывной случайной величины X, распределенной равномерно, в интервал от до (при условии что ) вычисляется по формуле:

.

2. Показательное распределение. Непрерывная случайная величина распределена по показательному закону, если ее плотность распре-деления имеет вид:

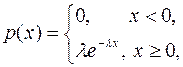
где .

Функция распределения для показательного распределения имеет вид:

На рисунках 3 и 4 представлены графики плотности и функции распределения показательного распределения.

Рис. 3. График плотности показательного распределения

Рис. 4. График функции распределения показательного распределения

Числовые характеристики:

.

Вероятность попадания непрерывной случайной величины X, распределенной по показательному закону, в интервал от до (при условии что 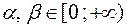) вычисляется по формуле:

.

3. Нормальное распределение. Непрерывная случайная величина распределена по нормальному закону, если ее плотность распре-деления имеет вид:

где .

Функция распределения для нормального распределения имеет вид:

,

где ,

или

,

где .

На рисунках 5 и 6 представлены графики плотности и функции распределения нормального распределения.

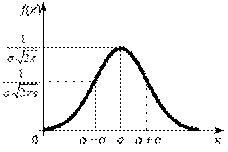Рис. 5. График плотности нормального распределения

Рис.6. График функции распределения нормального распределения

Числовые характеристики:

.

Вероятность попадания непрерывной случайной величины X, распределенной по нормальному закону, в интервал от до вычисляется по формуле:

или

.

3. РАСЧЕТНЫЕ ЗАДАНИЯ

Задание 1

1.1. В коробке лежат внешне одинаковые конфеты, из которых 12 штук с шоколадной начинкой, а 5 – с фруктовой. Из коробки наудачу взята одна конфета. Найти вероятность того, что она с шоколадной начинкой.

1.2. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 6.

1.3. В револьвере находится 2 пули, всего мест в барабане 6. Какова вероятность того, что револьвер выстрелит пулей при первом выстреле?

1.4. Из 7-ми гномов у 3-х красные колпаки, у 2-х – зеленые и у 2-х – желтые. Один из гномов теряет свой колпак. Какова вероятность, что этот колпак был зеленым?

1.5. У Деда Мороза в мешке лежит 30 подарков, которые он достает из мешка наудачу. В каждом подарке помимо конфет лежит одна игрушка: в 10-ти подарках – куклы, в остальных – машины. Какова вероятность того, что Оля получит подарок с куклой, если 7 подарков с куклами и 3 подарка с машинами Дед Мороз уже подарил?

1.6. В магазине на полке стоит 28 свежих пачек кефира и две просроченных. Какова вероятность того, что покупатель, купивший наудачу пачку кефира, не отравится?

1.7. Студент, готовясь к экзамену, выучил лишь 17 билетов из 100. Какова вероятность того, что студенту придется идти на пересдачу?

1.8. В конном забеге принимали участие 3 белых коня, 4 черных и один рыжий. Найти вероятность того, что первым к финишу придет белый конь.

1.9. Какова вероятность того, что наудачу выбранное число, от 40 до 70 включительно, делится на 6?

1.10. В книге 657 страниц. Известно, что имеется 7 опечаток (не более одной на странице). Какова вероятность того, что на наудачу выбранной странице окажется опечатка?

1.11. В аудитории находится 25 крепких стульев и 18 шатких. Найти вероятность того, что студент, зашедший в аудиторию и выбиравший место наудачу, сядет на хороший стул.

1.12. В беспроигрышной лотерее среди призов 26 леденцов, 12 карандашей, 5 книг, 50 статуэток и 1 мягкая игрушка. Найти вероятность выигрыша книги.

1.13. В студенческой группе 26 человек. Из них контрольную работу по математике 7 человек написали на «5», 10 человек на «4», остальные на «3». Найти вероятность того, что наудачу взятая работа окажется написанной на «3».

1.14. В магазине на продажу выставлены 25 телефонов китайского производства, среди которых 10 телефонов из Германии и 3 телефона из России. Найти вероятность того, что покупатель, не знающий страну-производителя телефона, купит телефон, произведенный в Германии.

1.15. В ювелирном магазине имеется 50 колец. 10 колец 15-го размера, 25 – 16-го, остальные – 17-го размера. Найти вероятность того, что наудачу взятое кольцо окажется 17-го размера.

1.16. В коробке 5 желтых и 8 белых мелков. Найти вероятность того, что после того, как из коробки наудачу взяли один мелок, все желтые мелки останутся в коробке.

1.17. В книге 564 страницы. Найти вероятность того, что наудачу открытая страница окажется из промежутка от 34 до 115 страницы включительно.

1.18. В магазине продается 84 фена фирмы «Philips» и 95 фенов фирмы «Samsung». Какова вероятность того, что наудачу взятый фен окажется произведенным фирмой «Philips»?

1.19. В оптике продается 5 пар очков с красной оправой, 15 – с черной и 2 – с белой. Найти вероятность того, что наудачу взятые очки будут с черной оправой.

1.20. В автобусе 20 пассажиров, из которых 25 % – женщины. На остановке выходит один человек. Какова вероятность того, что это не женщина?

1.21. В парке 100 деревьев, из которых 10 посажены 30 лет назад, остальные – 50 лет назад. Найти вероятность того, что наудачу выбранное дерево окажется посаженным 50 лет назад.

1.22. У преподавателя на столе 26 проверенных курсовых работ, 6 из которых оценены на «5», 10 – на «4», остальные на – «3». Какова вероятность того, что наудачу взятая работа окажется написанной на «3»?

1.23. В корзине лежит 20 белых грибов и один мухомор. Найти вероятность того, что наудачу выбранный гриб окажется мухомором.

1.24. В городе проживает 50 000 человек, из них 10 000 – лица пожилого возраста. Какова вероятность того, что наудачу выбранный человек окажется не пожилым?

1.25. Около остановки стоят 4 такси черного и 3 такси желтого цвета. Человек наудачу выбирает один автомобиль и уезжает. Какова вероятность того, что он уехал на желтом такси?

1.26. Какова вероятность того, что число на вырванном наудачу листке нового календаря високосного года кратно пяти?

1.27. Из полной игры лото наудачу извлекается один бочонок. На бочонках написаны цифры от единицы до 90 включительно. Какова вероятность того, что на извлеченном бочонке написано простое число?

1.28. В коллекции 200 монет, из которых 25 монет датированы XVIII веком. Какова вероятность того, что наудачу выбранная монета датирована XVIII веком?

1.29. Какова вероятность того, что кость, извлеченная из полного набора домино, имеет сумму очков, равную пяти?

1.30. В группе 6 юношей и 18 девушек. По жребию разыгрывается один билет в театр. Какова вероятность того, что билет получит девушка?

Задание 2

2.1. Из колоды в 36 карт наудачу извлекают две. Какова вероятность того, что среди вынутых карт нет тузов?

2.2. У Красной Шапочки в корзине лежит 5 пирожков с капустой, 4 – с картошкой и 7 – с повидлом. Когда она приходит к бабушке, та съедает 2 пирожка. Какова вероятность того, что она съела пирожки с картошкой?

2.3. В магазине из имеющихся 12 видов леденцов 5 – с апельсиновым вкусом. Какова вероятность того, что из 5-ти купленных леденцов различного вида ни одного не окажется с апельсиновым вкусом?

2.4. У садовода есть 5 белых и 6 красных луковиц тюльпанов, из которых он наудачу сажает 4 луковицы. Какова вероятность того, что на клумбе будут расти только красные тюльпаны?

2.5. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна крестовая карта.

2.6. Набирая номер телефона, абонент забыл 3 цифры и набрал их наудачу. Найти вероятность того, что он набрал нужные цифры.

2.7. Среди 20-ти денежных купюр 4 фальшивых. Какова вероятность того, что наудачу взятые 3 купюры окажутся фальши-выми?

2.8. В спортивный магазин поступили женские коньки: 2 пары 35-го, 6 – 36-го, 8 – 37-го, 7 – 39-го и 3 пары 40-го размера. Какова вероятность того, что наудачу взятые 2 пары коньков окажутся 36-го размера?

2.9. Среди 32-х дисков с фильмами 10 – мелодрамы, 12 – комедии, 3 – драмы, 4 – триллеры, остальные – ужасы. Какова вероятность того, что наудачу взятые 3 диска окажутся с ужасами?

2.10. После новогодних праздников на допросе в милиции сидит 5 человек в костюмах Дедов Морозов, трое из них – переодетые грабители. Какова вероятность того, что наудачу выбранные два Деда Мороза окажутся грабителями?

2.11. В кошельке с монетами лежит 2 монеты номиналом в 10 руб., 5 – 5 руб. и 3 – 1 руб. Из кошелька случайно берутся три монеты. Какова вероятность того, что сумма выбранных монет равна 12 руб.?

2.12. У ребенка 5 кубиков с буквами: А, К, Б, Л, У. Какова вероятность того, что из трех выбранных наугад кубиков ребенок соберет слово «ЛУК»?

2.13. Маша выбрала 12 конфет, 7 из которых – с орехами, и решила, что без вреда для фигуры и для повышения жизненного тонуса она съест сегодня 6 с орехами, а остальные – через день. Но в сумке конфеты перемешались, и ей пришлось съесть 6 наудачу выбранных конфет. Какова вероятность того, что все они были с орехами?

2.14. Накануне 8 марта в цветочном магазине осталось 25 роз, из которых 13 – белых, а остальные – красные. Мужчина для подарка жене наудачу купил 7 роз. Найти вероятность того, что они все – белые.

2.15. С отдыха на море Катя привезла 17 ракушек, 13 из которых подняты с морского дна, а остальные куплены. Для подарка подруге Катя выбрала 3 ракушки. Найти вероятность того, что только одна из них поднята со дна моря.

2.16. Группа, состоящая из пяти юношей и семи девушек, распределяет по жребию четыре билета в театр. Какова вероятность того, что в числе получивших билеты окажется три девушки и один юноша?

2.17. Среди 18-ти шампуней от перхоти, предложенных Диме консультантом в аптеке, только 10 эффективно способствуют исчезновению перхоти. Дима наудачу купил 5 шампуней. Какова вероятность того, что среди купленных хотя бы один шампунь, эффективно способствуют исчезновению перхоти?

2.18. В магазине работают 10 продавцов, из них 6 – женщины. Найти вероятность того, что в укомплектованную из трех человек смену войдут только мужчины.

2.19. В магазине бытовой техники «Эльдорадо» выставлено на продажу 18 видов стиральных машин, в 10-ти из которых отсутствует режим легкой глажки. В течение дня было куплено 7 стиральных машин. Какова вероятность того, что среди них только 3 окажутся с режимом легкой глажки?

2.20. Собрание, на котором присутствуют 20 человек, в том числе 5 женщин, выбирает делегацию из трех человек. Найти вероятность того, что в делегацию войдут две женщины и один мужчина.

2.21. Из колоды в 36 карт наугад выбирают три карты. Какова вероятность того, что среди них окажутся 2 туза?

2.22. В оптику завезли 15 видов линз, среди которых 4 вида – цветные. Посетитель приобрел 3 пары различных линз. Какова вероятность того, что среди них только одна пара цветных линз?

2.23. Студент успел подготовить к экзаменам 20 вопросов из 25-ти. Какова вероятность того, что из трех наудачу выбранных вопросов студент знает все?

2.24. В магазин завезена партия футболок (7 штук), все разного размера. Какова вероятность того, что они будут развешаны в порядке возрастания размеров?

2.25. В коробке с игрушками у Пети лежат 20 машинок, у шести из которых отломаны колеса. Петя с тремя друзьями случайным образом берут по одной машинке для игры. Какова вероятность того, что у взятых машинок все колеса окажутся на месте?

2.26. На столе стоят внешне не различимые 7 бокалов с шампанским и 5 бокалов с газированной водой. Водитель автобуса наудачу выпил 3 бокала. Какова вероятность того, что после этого он сможет сесть за руль?

2.27. С помощью клавиатуры компьютера наудачу набираются 4 разные буквы. Какова вероятность того, что все они окажутся согласными?

2.28. В связке находится 12 ключей, среди которых один от сейфа. Наудачу взяли 3 ключа. Какова вероятность того, что среди них окажется ключ от сейфа?

2.29. В кармане студента лежало 13 шпаргалок, среди которых 7 соответствовали вопросом экзамена. Студент наудачу вытащил 5 шпаргалок. Какова вероятность того, что они ему не помогут?

2.30. В магазине продается 15 сумок, из них 4 – с дефектами. Зашедшие в магазин две подруги купили себе каждая по сумке. Какова вероятность того, что обе сумки окажутся без дефектов?

Задание 3

3.1. Из отрезка [-2; 2] наудачу взято одно число х, а из отрезка [0; 3] – другое y. Какова вероятность того, что их сумма x + y не больше двух, а разность x - y – неотрицательная?

3.2. Из отрезка [0; 3] наудачу взяты два числа: x, y. Какова вероятность того, что их произведение xy не меньше двух, а частное x/y – не больше двух?

3.3. Из отрезка [0; 2] наудачу взято одно число х, а из отрезка [0;4] – другое y. Какова вероятность того, что их сумма x + y не больше двух, а квадрат первого числа не больше второго числа?

3.4. Из отрезка [-2; 4] наудачу взяты два числа x, y. Какова вероятность того, что их сумма x + y не меньше одного, а произведение xy – не больше одного?

3.5. Наудачу взяты два положительных числа x, y, каждое из которых не превосходит пяти. Какова вероятность того, что их произведение xy и частное x/y не больше трех?

3.6. Из отрезка [-4; 0] наудачу взяты два числа: x, y. Какова вероятность того, что их произведение xy не больше четырех, а частное x/y – не меньше двух?

3.7. Из отрезка [1; 5] наудачу взяты два числа: x, y. Какова вероятность того, что их сумма x + y не меньше четырех, а произведение xy – не меньше трех?

3.8. Из отрезка [-1; 3] наудачу взяты два числа: x, y. Какова вероятность того, что их сумма x + y не меньше двух, а частное x/y – не больше трех?

3.9. Наудачу взяты два положительных числа: x, y, каждое из которых не превышает трех. Какова вероятность того, что их сумма x + y не больше трех, а произведение xy – не больше двух?

3.10. Из отрезка [0; 4] наудачу взяты два числа: x, y. Какова вероятность того, что их сумма x + y не больше трех, а разность x - y – не больше двух?

3.11. Из отрезка [1; 2] наудачу взято одно число х, а из отрезка [0; 2] – другое y. Какова вероятность того, что их сумма x + y не больше трех, а произведение xy – не меньше одного?

3.12. Из отрезка [-2; 4] наудачу взяты два числа: x, y. Какова вероятность того, что их сумма x + y не меньше двух, а произведение xy – не больше одного?

3.13. Наудачу взяты два положительных числа: x, y, каждое из которых не превышает двух. Какова вероятность того, что их произведение xy не больше двух, а частное x / y – не больше одного?

3.14. Наудачу взяты два положительных числа: x, y, каждое из которых не превышает трех. Какова вероятность того, что их сумма x + y не больше двух и первое число не меньше квадрата второго числа?

3.15. Наудачу взяты два отрицательных числа: x, y, каждое из которых не меньше минуса двух. Какова вероятность того, что их сумма x + y не больше минус двух, а произведение xy – не больше двух?

3.16. Из отрезка [-2; 5] наудачу взяты два числа: x, y. Какова вероятность того, что их сумма x + y не меньше одного, а произведение xy – не больше двуx?

3.17. Из отрезка [-2; 2] наудачу взято одно число х, а из отрезка [0; 3] – другое y. Какова вероятность того, что их сумма x + y не меньше двух, а разность x - y – неположительная?

3.18. Из отрезка [0; 4] наудачу взяты два числа: x, y. Какова вероятность того, что их сумма x + y не меньше трех, а разность x - y – не меньше двух?

3.19. Наудачу взяты два положительных числа: x, y, каждое из которых не превышает единицы. Какова вероятность того, что их сумма x + y не больше единицы, а разность x - y – неотрицательная?

3.20. Из отрезка [0; 3] наудачу взяты два числа: x, y. Какова вероятность того, что их произведение xy и частное x/y не больше двух?

3.21. Из отрезка [-2; 2] наудачу взято одно число х, а из отрезка [2; 4] – другое y. Какова вероятность того, что их сумма x + y не меньше двух, а произведение xy – не больше двух?

3.22. Наудачу взяты два положительных числа: x, y, каждое из которых не превышает трех. Какова вероятность того, что их сумма x + y не больше трех, а произведение xy – не меньше единицы?

3.23. Из отрезка [-2; 4] наудачу взяты два числа: x, y. Какова вероятность того, что их сумма x + y не меньше двух, а разность x - y – не больше трех?

3.24. Из отрезка [-2; 2] наудачу взято одно число х, а из отрезка [0; 3] – другое y. Какова вероятность того, что их сумма x + y не больше двух, а разность x - y – неположительная?

3.25. Изотрезка [-2; 2] наудачу взяты два числа: x, y. Какова вероятность того, что их разность x - y неотрицательная, а произведение xy – не больше минус единицы?

3.26. Наудачу взяты два отрицательных числа: x, y, каждое из которых не меньше минус четырех. Какова вероятность того, что их сумма x + y не меньше минус четырех, а частное x/y – не меньше двух?

3.27. Из отрезка [-2; 2] наудачу взято одно число х, а из отрезка [0; 3] – другое y. Какова вероятность того, что их сумма x + y не меньше двух, а разность x - y – неотрицательная?

3.28. Наудачу взяты два положительных числа: x, y, каждое из которых не превышает пяти. Какова вероятность того, что их произведение xy не меньше трех, а частное x/y – не больше трех?

3.29. Из отрезка [-4; 0] наудачу взяты два числа:: x, y. Какова вероятность того, что их произведение xy не меньше четырех, а частное x/y – не меньше двух?

3.30. Из отрезка [1; 5] наудачу взяты два числа: x, y. Какова вероятность того, что их сумма x + y не меньше трех, а произведение xy – не больше четырех?

Задание 4

4.1. Вероятности того, что нужное лекарство есть в наличии в первой, второй, третьей, четвертой аптеках соответственно равны 0,5; 0,6; 0,7; 0,8. Найти вероятность того что нужное лекарство есть в наличии:

А: {только в трех аптеках};

B: {хотя бы в одной аптеке};

С: {только в третьей аптеке}.

4.2. В детской команде по хоккею вероятность того, что на тренировке основной хоккеист попадет в ворота с первого раза, равна 0,5, а запасной – 0,3. Найти вероятность того, что при первом ударе в ворота попадет:

A: {только один из хоккеистов};

B: {хотя бы один из хоккеистов};

С: {только первый хоккеист}.

4.3. Ученик ищет нужную ему книгу в четырех книжных магазинах. Вероятность того, что нужная книга окажется в магазинах «Буква», «Книгомир», «Учебная книга» и «Школьник» соответствен-но равны 0,2; 0,3; 0,4; 0,5. Найти вероятность того, что книга будет в продаже:

A: {только во втором магазине};

B: {менее чем в двух магазинах};

C: {хотя бы в одном магазине}.

4.4. Нужная студенту информация содержится на одном из трех сайтов. Вероятность того, что он найдет ее на первом, втором и третьем сайтах соответственно равна 0,7; 0,8; 0,9. Найти вероятность того, что нужная информация есть:

A: {только на одном сайте};

B: {хотя бы на одном сайте};

C: {не менее чем на двух сайтах}.

4.5. Витя и Женя метают дротики в мишень. Вероятность того, что с первого раза Витя попадет в мишень равна 0,5; Женя – 0,4. Найти вероятность того, что при первой попытке в мишень попадут:

A: {оба мальчика};

B: {хотя бы один мальчик};

С: {только Женя}.

4.6. В предстоящем турнире командой «Юпитер» будет сыгранно четыре матча, вероятности выигрышей в каждом матче соответственно равны 0,4; 0,5; 0,6; 0,8. Найти вероятность того, что команда перейдет в следующий тур, если для перехода достаточно выиграть:

A: {один матч};

B: {только первый матч};

C: {хотя бы один матч}.

4.7. Для того, чтобы получить на экзамене по математике «отлично» автоматом, необходимо написать две контрольные на «5» и сдать типовой расчет, а чтобы получить «хорошо» – необходимо написать только одну контрольную на «5» и сдать типовой расчет. Студентка Маша напишет первую контрольную на «5» с вероятность 0,6, вторую контрольную – с вероятностью 0,4, а типовой расчет сдаст с вероятностью 0,7. Найти вероятность того, что Маша:

A: {получит на экзамене «отлично» автоматом};

B: {получит на экзамене «хорошо» автоматом}

C: {напишет только одну контрольную на «5» и не сдаст типовой расчет}.

4.8. Студент решает контрольную работу из четырех задач. Первую, вторую, третью и четвертую задачи он решит соответственно с вероятностями 0,2; 0,6; 0,5 и 0,3. Для того, чтобы получить зачет, студент должен решить хотя бы три задачи. Найти вероятность того, что студент:

A: {получит зачет};

B: {решит хотя бы одну задачу};

C: {решит только третью задачу}.

4.9. Автомобилист ищет нужные запчасти в трех автомагазинах. Вероятность того, что деталь имеется в наличии в первом магазине, равна 0,3; во втором магазине – 0,6; в третьем магазине – 0,5. Найти вероятность того, что деталь имеется:

A: {хотя бы в одном магазине};

B: {только в двух магазинах};

C: {только во втором магазине}.

4.10. В металле могут содержаться одна, несколько или ни одной из четырех примесей. Вероятности содержания в металле каждой из них соответственно равны 0,3; 0,4; 0,5; 0,6. Найти вероятность того, что в металле содержатся:

A: {три примеси};

B: {только третья примесь};

C: {не более двух примесей}.

4.11. Для того чтобы студент смог получить повышенную стипендию ему нужно сдать на «отлично» не менее трех экзаменов из четырех, а полуповышенную – хотя бы один на «отлично»». Студент сдаст каждый из четырех экзаменов на «отлично» с вероятностями 0,3; 0,9; 0,7; 0,5 соответственно. Найти вероятность того, что студент:

А: {получит повышенную стипендию};

B: {получит полуповышенную стипендию};

С: {сдаст на «отлично» только третий экзамен}.

4.12. Швея ищет определенную ткань в трех магазинах. Вероят-ности того, что ткань есть в магазинах «Швея», «Мир ткани» и «Портняжка» соответственно равны 0,7; 0,8; 0,6. Найти вероятность, того что ткань есть:

А: {только в магазинах «Швея» и «Портняжка»};

В: {во всех трех магазинах};

С: {хотя бы в одном}.

4.13. Дети играют в онлайн игру. Персонаж Васи дойдет до конца уровня с вероятностью 0,6; персонаж Игоря – 0,5; персонаж Антона – 0,3. Найти вероятность того, что:

A: {хотя бы один дойдет до конца};

B: {только двое дойдут до конца};

С: {только персонаж Игоря дойдет до конца}.

4.14. На тренировке футбольной команды, основной игрок попадает в ворота с первого раза с вероятностью 0,7; а запасной – 0,4. Найти вероятность того, что при первом ударе в ворота:

А: {не попадет ни один из футболистов};

В: {попадет хотя бы один};

С: {попадет только первый}.

4.15. Производство состоит из четырех последовательных этапов, на каждом из которых вероятности выхода из строя оборудования в течение ближайшего месяца соответственно равны 0,4; 0,6; 0,7 и 0,9. Найдите вероятность того, что за месяц:

A: {случиться хотя бы одна остановка};

B: {ни одной остановки не случиться};

C: {случиться не более двух остановок}.

4.16. Трое пациентов реабилитируются после некоторой операции. Вероятность того, что первый пациент полностью восстановится за неделю равна 0,7; второй – 0,6; третий – 0,9. Найти вероятность того, что:

Не нашли, что искали? Воспользуйтесь поиском: