ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Некоторые стандартные распределения непрерывных случайных величин 5 страница
14.10. 
14.11.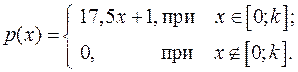 
14.12.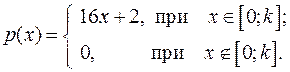 
14.13. 
14.14.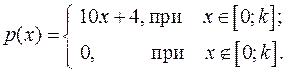 
14.15.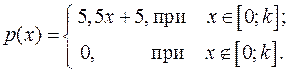 
14.16.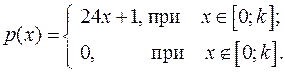 
14.17.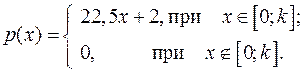 
14.18. 
14.19.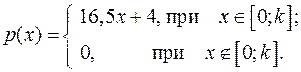 
14.20.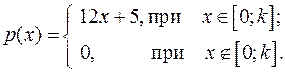 
14.21.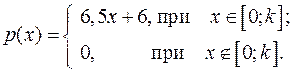 
14.22. 
14.23.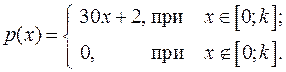 
14.24.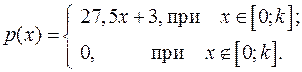 
14.25.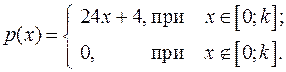 
14.26.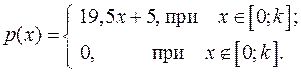 
14.27.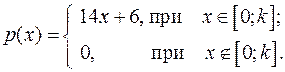 
14.28.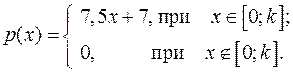 
14.29.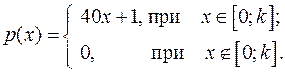 
14.30.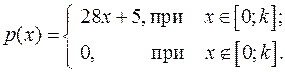 
Задание 15
Дана плотность распределения случайной величины X. Найти плотность распределения 
, а, математическое ожидание 
, дисперсию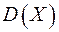 
, среднее квадратическое отклонение 
, вероят-ность выполнения неравенства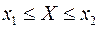 
. Построить график плот-ности и изобразить на нем найденную вероятность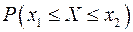 
.
15.1.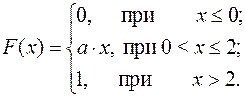 
15.2.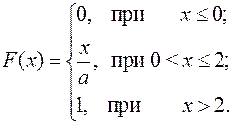 
15.3.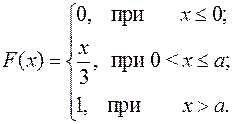 
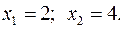
15.4. 
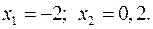
15.5. 
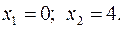
15.6. 
15.7.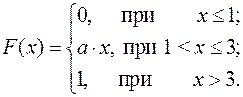 
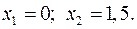
15.8.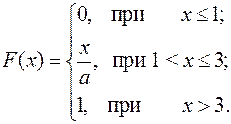 
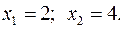
15.9.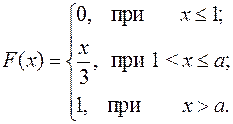 
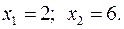
15.10.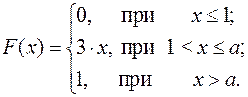 
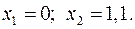
15.11.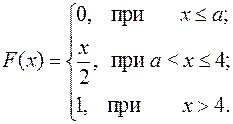 
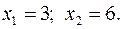
15.12. 
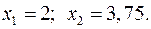
15.13.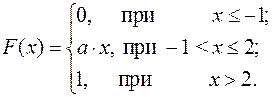 
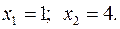
15.14.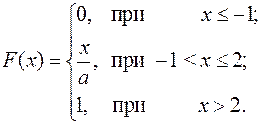 
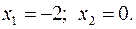
15.15. 
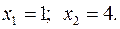
15.16.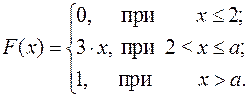 
15.17.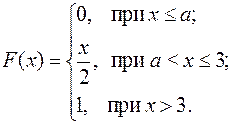 
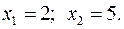
15.18.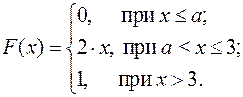 
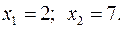
15.19.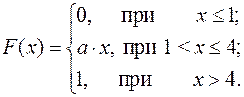 
15.20. 
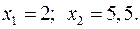
15.21.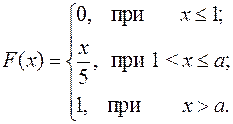 
15.22. 
15.23.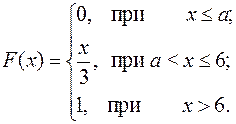 
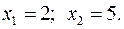
15.24.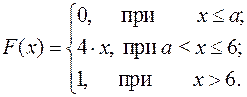 
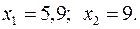
15.25. 
15.26.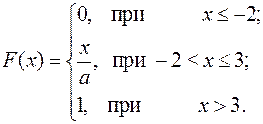 
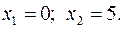
15.27.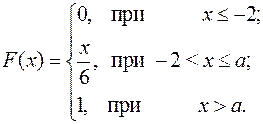 
15.28.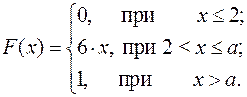 
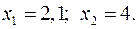
15.29. 
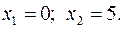
15.30. 
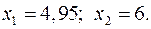
Задание 16
Известно математическое ожидание показательного распределения. Найти плотность распределения , интегральную функцию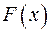 
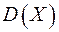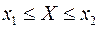, дисперсию , среднее квадратическое откло-нение , вероятность выполнения неравенства . Построить график плотности и изобразить на нем найденную вероятность .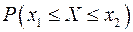
16.1. 
16.2.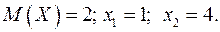 
16.3. 
16.4.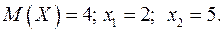 
16.5.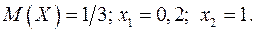 
16.6. 
16.7.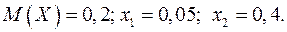 
16.8.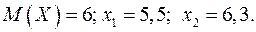 
16.9. 
16.10. 
Известна дисперсия 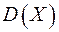показательного распределения. Найти плотность распределения , интегральную функцию 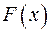, математическое ожидание , среднее квадратическое отклоне-ние , вероятность выполнения неравенства 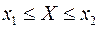. Постро-ить график плотности и изобразить на нем найденную вероятность .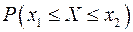
16.11. 
16.12. 
16.13.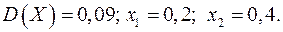 
16.14. 
16.15.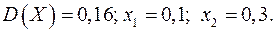 
16.16.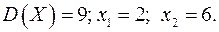 
16.17. 
16.18.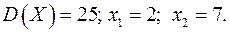 
16.19.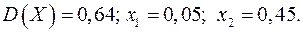 
16.20.
Известно среднее квадратическое отклонение показательного распределения. Найти плотность распределения , интегральную функцию 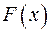, математическое ожидание , дисперсию 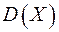, вероятность выполнения неравенства 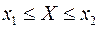. Построить график плотности и изобразить на нем найденную вероятность .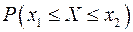
16.21. 
16.22.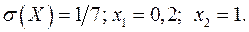 
16.23.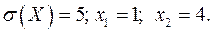 
16.24.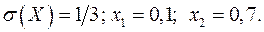 
16.25.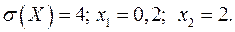 
16.26.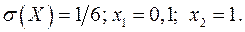 
16.27.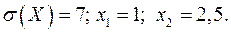 
16.28.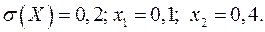 
16.29.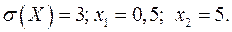 
16.30. 
Задание 17
Плотность распределения вероятностей случайной величины Х имеет вид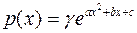 
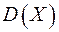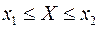. Найти: γ, математическое ожидание , дисперсию , среднее квадратическое отклонение , функцию распределения случайной величины Х, вероятность выполнения неравенства . Построить график плотности и изобразить на нем найденную вероятность .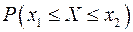
17.1.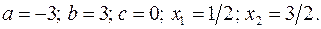 
17.2. 
17.3.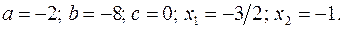 
17.4.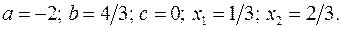 
17.5.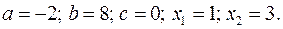 
17.6.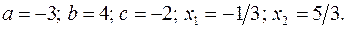 
17.7.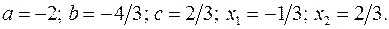 
17.8. 
17.9.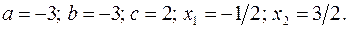 
17.10. 
17.11. 
17.12.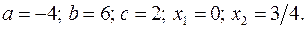 
17.13.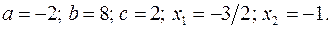 
17.14. 
17.15.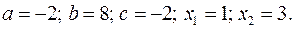 
17.16.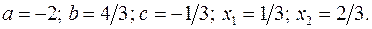 
17.17.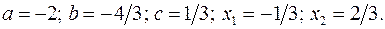 
17.18.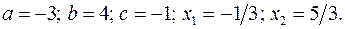 
17.19.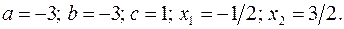 
17.20.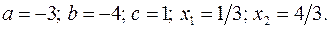 
17.21.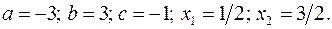 
17.22. 
17.23.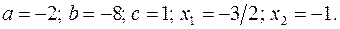 
17.24. 
17.25.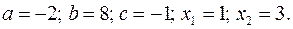 
17.26.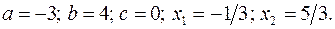 
17.27. 
17.28.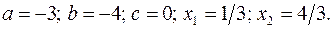 
17.29.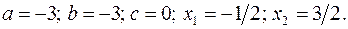 
17.30.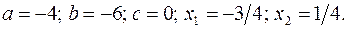 
ЛИТЕРАТУРА
1. Гмурман, В.Е. Теория вероятностей и математическая статистика: учебное пособие для вузов / В.Е. Гмурман. – М.: Юрайт, 2011. – 478 с.
2. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие для вузов / В.Е. Гмурман. – М.: Юрайт, 2011. – 403 с.
3. Письменный, Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам: курс лекций для вузов / Дмитрий Письменный. – М: Айрис-пресс, 2008. – 287 с.
4. Чудесенко, В.Ф. Сборник заданий по специальным курсам высшей математики. Типовые расчеты: учебное пособие / В.Ф. Чудесенко. – СПб.: Лань, 2005. – 124 с.
ПРИЛОЖЕНИЯ
Приложение А. Значение функции 
Таблица А
| x | ||||||||||
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,0044 | |||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
Приложение Б. Значение функции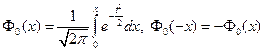 
Таблица Б
| x | ||||||||||
| 0,0 | 0,00000 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,34134 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,47725 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,49865 | 3,1 | 3,2 | 3,3 | 3,4 | |||||
| 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | ||||||
| 4,0 | ||||||||||
| 4,5 | ||||||||||
| 5,0 |
Не нашли, что искали? Воспользуйтесь поиском: