Движения материальной точки

Шарик М, рассматриваемый как материальная точка, перемещается по цилиндрическому каналу движущегося тела А (рис. 13-15). Найти уравнение относительного движения этого шарика х = f (t), приняв за начало отсчета точку О.

Тело А равномерно вращается вокруг неподвижной оси (в вариантах 2, 3, 4, 7, 10, 11, 14, 20, 23, 26 и 30 ось вращения вертикальна, в ва­риантах 1, 12, 15 и 25 ось вращения горизонтальна). В вариантах 5, 6, 8, 9, 13, 16, 17, 18, 19, 21, 22, 24, 27, 28 и 29 тело А движется поступа­тельно, параллельно вертикальной плоскости .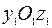

Найти также координату х и силу давления шарика на стенку канала при заданном значении 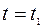. Данные, необходимые для выполнения 30-ти вариантов задания, приведены в табл. 2.

В задании приняты следующие обозначения: т − масса шарика М; 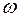− постоянная угловая скорость тела А (в вариантах 1−4, 7, 10−12, 14, 15, 20, 23, 25, 26, 30) или кривошипов В и 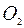С (в вариантах 6, 17, 22); с − коэффициент жесткости пружины, к которой прикреплен шарик М; − длина недеформированной пружины; f − коэффициент трения скольже­ния шарика по стенке канала; 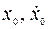− начальная координата и проекция начальной скорости на ось х.

Пример выполнения задания (рис. 16). Дано: рад/с; 30°; т = 0,05 кг; = 0,1 с; = 0,2 м; = 0 м/с; 0,01 Н/cм; 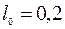м. Найти уравнение относительного движения шари-

ка М, а также координату x и силу давления шарика на стенку канала при заданном .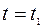

Решение. Свяжем подвижную систему отсчета с телом А, вращающимся вокруг неподвижной оси . При этом ось 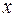направлена вдоль прямолинейного канала, по которому совершает относительное движение шарик М, в сторону удлинения пружины.

Переносным движением для шарика М является вращение подвижной системы отсчета вместе с телом А вокруг оси .

Относительное движение шарика М как материальной точки описывается векторным уравнением

. (1)

К шарику M приложены: сила тяжести 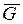, нормальная реакция стенки канала, которую целесообразно разложить на две взаимно перпендикулярные составляющие и , сила упругости пружины.

Модуль силы упругости определяется следующим образом:

,

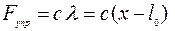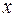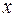где деформация пружины (при этом полагается, что в текущем положении шарика его координата в подвижной системе отсчета положительна, т. е. >0, а пружина растянута).

На относительное движение шарика М влияет перемещение подвижной системы отсчета и тела А, с которым эта система связана. Это влияние учитывается введением переносной и кориолисовой сил инерции.

Переносная сила инерции направлена противоположно переносному ускорению :

.

При равномерном переносном вращении тела A вокруг оси ускорение равно центростремительному ускорению точки М тела A. При этом модуль переносной силы инерции находится по формуле . Кориолисова сила инерции определяется из векторного выражения

где кориолисово ускорение; вектор угловой

скорости переносного вращения, направленный вдоль оси z₁ в соот-

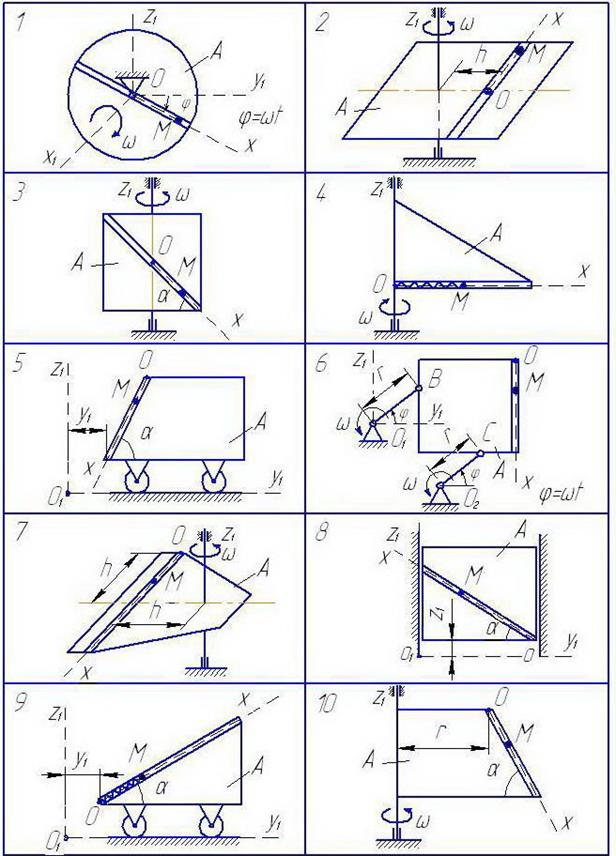
Рис. 13

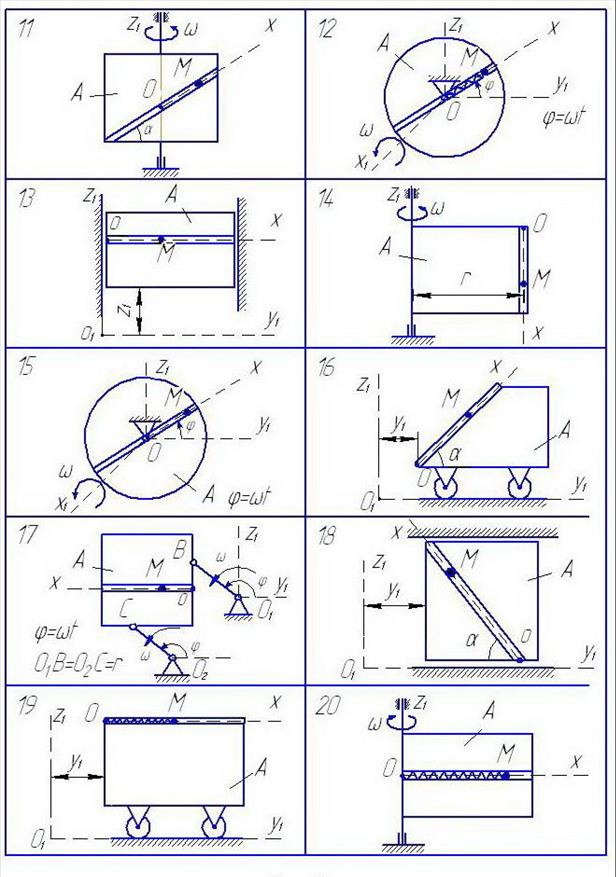
Рис. 14

Рис. 15

Рис. 16

ветствии с круговой стрелкой ; вектор относительной скорости шарика М (в текущий момент времени полагается, что проекция скорости 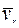на ось 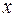положительна, т. е. >0). Направление вектора кориолисова ускорения 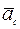определяется в соответствии с правилом векторного произведения 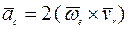: вектор 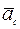направлен перпендикулярно плоскости , содержащей перемножаемые векторы и 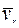, в ту сторону, откуда кратчайший поворот вектора до совмещения с вектором 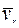виден происходящим против хода часовой стрелки. Кориолисова сила инерции направлена противоположно кориолисову ускорению 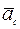и по модулю равна

°

.

Основное уравнение динамики относительного движения материальной точки (шарика М) в данном случае имеет вид

. (2)

Проектируя векторное уравнение (2) на ось 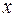, получим дифференциальное уравнение относительного движения шарика М вдоль оси :

;

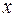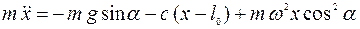
или

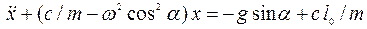. (3)

Уравнение (3) является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами, общее решение которого имеет вид

,

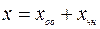где

− общее решение соответствующего однородного уравнения ;

− частное решение уравнения (3).

Составим характеристическое уравнение и найдем его корни:

;

.

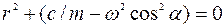Поскольку корни и характеристического уравнения являются действительными различными числами и , общее решение записывается в виде

.

Частное решение дифференциального уравнения (3) находим в форме .

Подставляя в уравнение (3), находим:

,

откуда

м.

Общее решение дифференциального уравнения (3) относительного движения шарика М получает вид

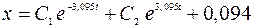. (4)

Для определения постоянных интегрирования 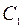и формируем, кроме того, функцию :

. (5)

Подставляя начальные условия (t = 0; м; )

в уравнения (4) и (5), получим:

;

,

откуда

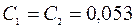м.

Уравнение относительного движения шарика М принимает вид

(м), (6)

а скорость его относительного движения выражается следующим образом:

(м/с). (7)

Для определения модулей составляющих и реакции стенки трубки при t = = 0,1 с выразим векторное уравнение (1) в проекциях на оси y и z. Учитывая, что вектор перпендикулярен этим осям, получаем:

;

.

Из этих уравнений находим

;

.

Для получения числовых значений N ₁ и N ₂ найдем координату

и проекцию относительной скорости шарика в заданный момент

времени с: м;

м/с.

Тогда

0,6 Н;

Н.

Реакция стенки трубки

Н.

Искомая сила давления шарика M на стенку канала по модулю равна найденной реакции и направлена в противоположную сторону ().

Ответ: (м); м; Н.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ

ТОЧКИ

Не нашли, что искали? Воспользуйтесь поиском: