
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Угловой скорости твердого тела
Однородная пластина H массой 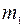 вращается вокруг вертикальной оси z с постоянной угловой скоростью
вращается вокруг вертикальной оси z с постоянной угловой скоростью 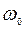 ; при этом в точке О желоба АВ пластины на расстоянии АО от точки А, отсчитываемом вдоль желоба, закреплена материальная точка К массой
; при этом в точке О желоба АВ пластины на расстоянии АО от точки А, отсчитываемом вдоль желоба, закреплена материальная точка К массой 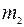 (рис. 23−27). В некоторый момент времени (t = 0) на систему начинает действовать пара сил с моментом
(рис. 23−27). В некоторый момент времени (t = 0) на систему начинает действовать пара сил с моментом 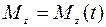 . При
. При  действие пары сил прекращается и далее пластина вращается по инерции с угловой скоростью
действие пары сил прекращается и далее пластина вращается по инерции с угловой скоростью  . В некоторый момент времени
. В некоторый момент времени 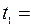 0 (новое начало отсчета времени) точка К (самоходная тележка) начинает относительное движение из точки О вдоль желоба АВ (в направлении к В) по закону ОК
0 (новое начало отсчета времени) точка К (самоходная тележка) начинает относительное движение из точки О вдоль желоба АВ (в направлении к В) по закону ОК 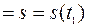 .
.
Определить значения  и
и  угловой скорости пластины в моменты времени
угловой скорости пластины в моменты времени 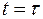 и
и 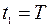 , пренебрегая сопротивлениями вращению пластины и массой вертикального вала. Необходимые для решения данные приведены в табл. 4, а требующиеся для расчетов моменты инерции тел – в табл. 5.
, пренебрегая сопротивлениями вращению пластины и массой вертикального вала. Необходимые для решения данные приведены в табл. 4, а требующиеся для расчетов моменты инерции тел – в табл. 5.
Примечание. В таблице 4 знак минус перед  и
и 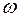 соответствует направлению вращения часовой стрелки, если смотреть со стороны положительного направления оси z.
соответствует направлению вращения часовой стрелки, если смотреть со стороны положительного направления оси z.
Пример выполнения задания (рис. 28). Дано: 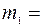
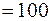 кг;
кг; 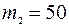 кг;
кг;  H·м;
H·м; 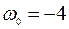 рад/с;
рад/с; 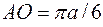 м;
м;
 м;
м; 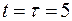 с;
с;  м;
м; 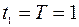 с.
с.
Определить 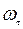 и
и 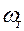 , считая тело H однородной круглой пластиной, а вал ED невесомым.
, считая тело H однородной круглой пластиной, а вал ED невесомым.
Решение. Объект исследования – механическая система, состоящая из пластины Н с валом и материальной точки К. Для решения задачи воспользуемся теоремой об изменении кинетического момента механической системы
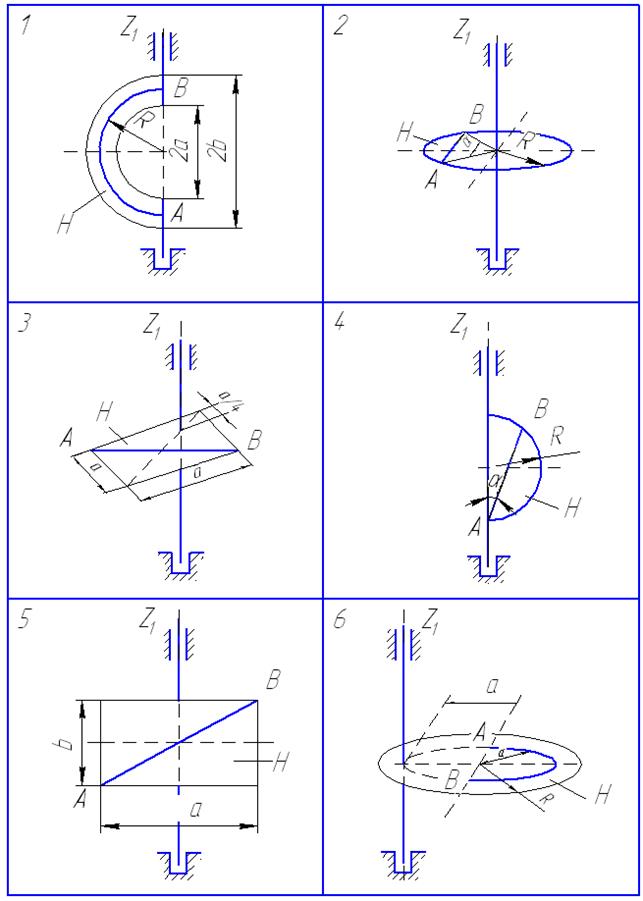 Рис. 23
Рис. 23
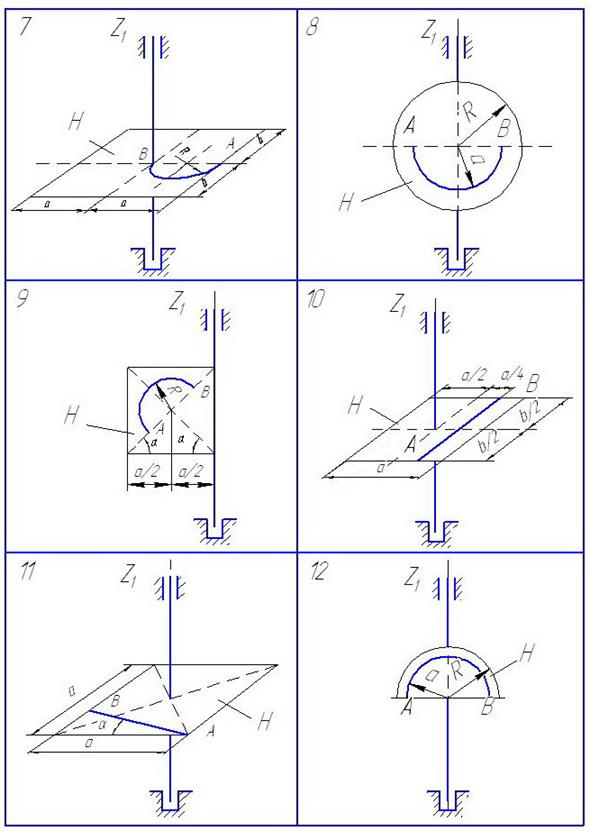
Рис. 24
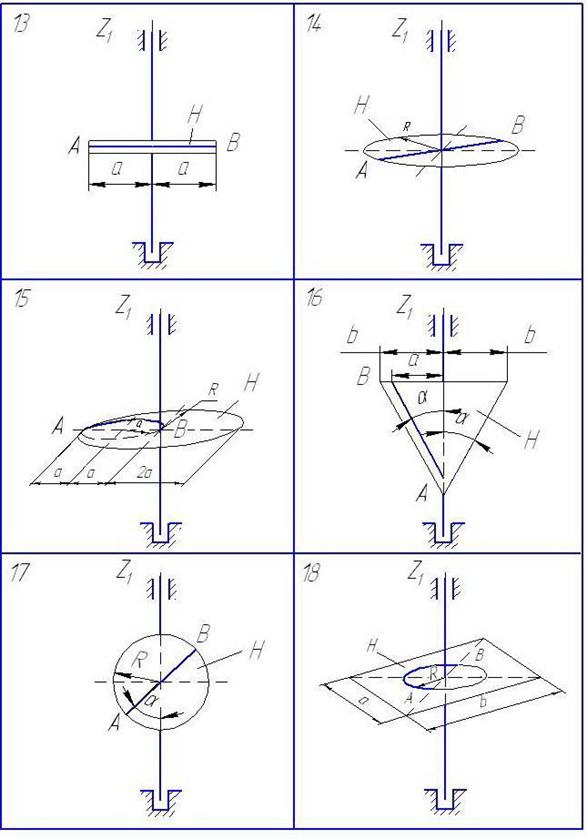
Рис.25
 Рис. 26
Рис. 26
 Рис. 27
Рис. 27
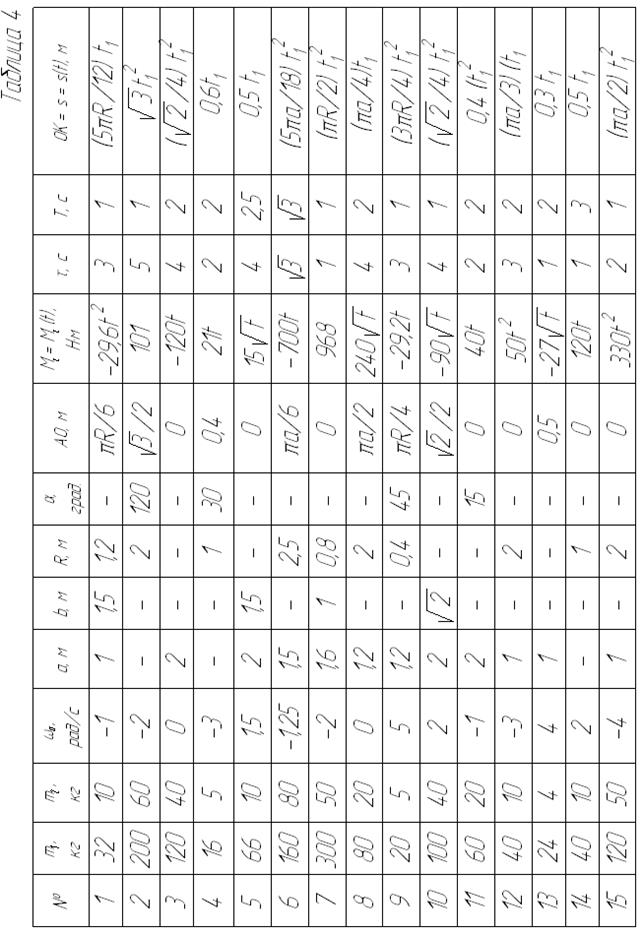
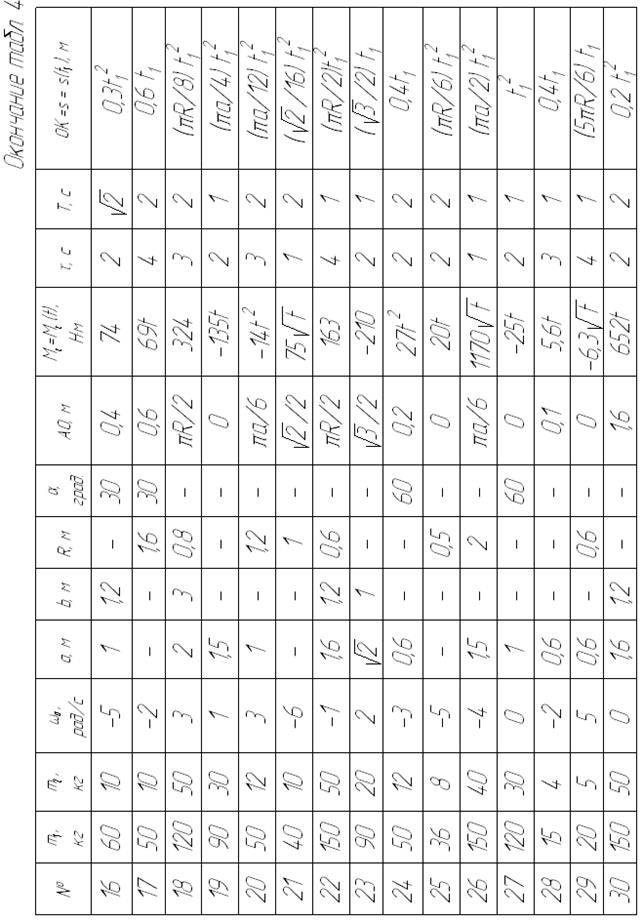
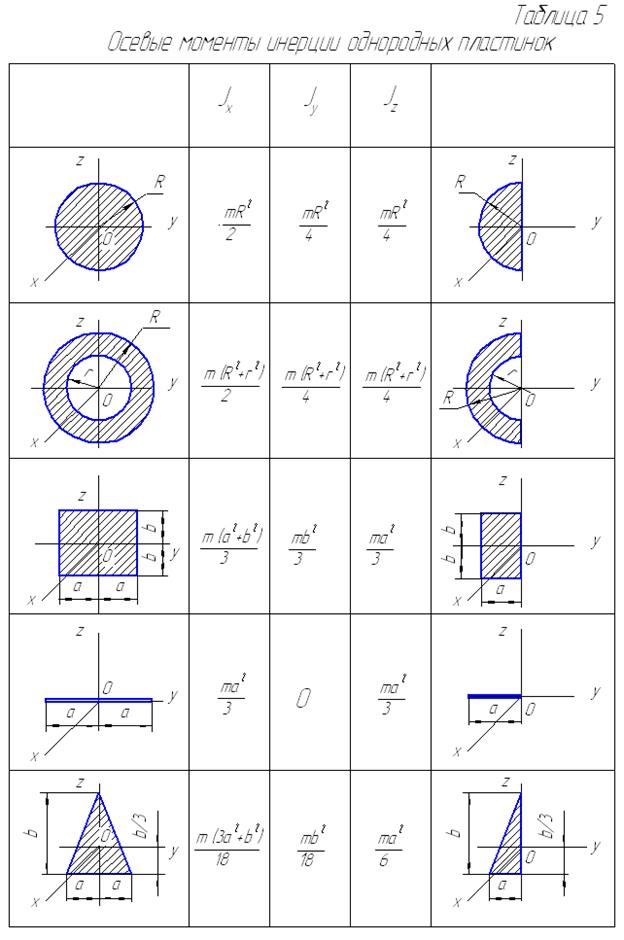
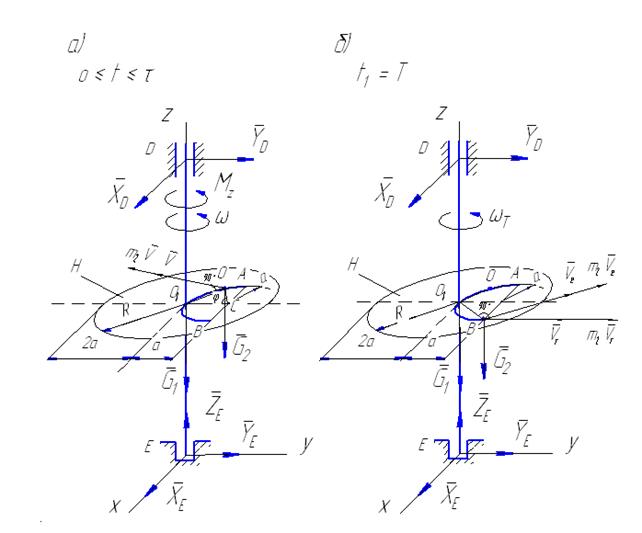 Рис. 28
Рис. 28
 , (1)
, (1)
где  кинетический момент рассматриваемой системы относительно оси z;
кинетический момент рассматриваемой системы относительно оси z; 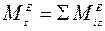 − главный момент внешних сил, приложенных к системе, относительно этой оси.
− главный момент внешних сил, приложенных к системе, относительно этой оси.
На систему за время от  до t =
до t = 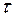 действуют сила тяжести
действуют сила тяжести 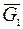 пластины, сила тяжести
пластины, сила тяжести 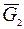 точки К, пара сил с моментом
точки К, пара сил с моментом  , а также реакции подпятника Е и подшипника D (рис. 28, а).
, а также реакции подпятника Е и подшипника D (рис. 28, а).
Предположим, что вращение пластины Н происходит против хода часовой стрелки, если смотреть со стороны положительного направления оси z; будем считать это направление вращения положительным при определении знаков кинетических моментов.
Найдем выражение кинетического момента 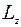 системы, кото-
системы, кото-
рый складывается из кинетического момента  пластиныи кинетического момента
пластиныи кинетического момента  точки К, являющегося моментом ее количества движения относительно оси
точки К, являющегося моментом ее количества движения относительно оси 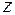 , т. е.
, т. е.  .
.
Момент инерции 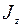 круглой однородной пластиныотносительно оси вращения, проходящей через ее центр масс, равен
круглой однородной пластиныотносительно оси вращения, проходящей через ее центр масс, равен 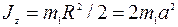 . Тогда кинетический момент пластины
. Тогда кинетический момент пластины 
 .
.
Материальная точка К, закрепленная в точке О пластины, имеет скорость 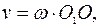 где
где  − хорда окружности радиуса а, стягивающая дугу
− хорда окружности радиуса а, стягивающая дугу  длины
длины 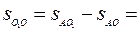
 , поэтому центральный угол
, поэтому центральный угол 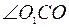
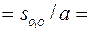
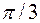 и треугольник
и треугольник 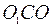 является равносторонним со стороной, равной
является равносторонним со стороной, равной 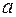 (рис. 28, a). Тогда
(рис. 28, a). Тогда 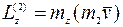
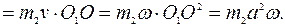
Таким образом,
 .
.
Главный момент внешних сил 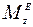 равен вращающему моменту
равен вращающему моменту  , так как остальные силы системы момента относительно оси z не создают.
, так как остальные силы системы момента относительно оси z не создают.
Уравнение (1), выражающее теорему об изменении кинетического момента, примет вид:
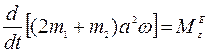 , (2)
, (2)
где 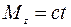 (c = 240 Н·м/с).
(c = 240 Н·м/с).
В уравнении (2) разделим переменные
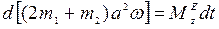
и проинтегрируем левую и правую части уравнения в соответствующих пределах
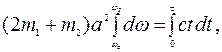
 (3)
(3)
Из уравнения (3) получим
 рад/с.
рад/с.
После прекращения действия момента  пластина H вращается по инерции с угловой скоростью
пластина H вращается по инерции с угловой скоростью  ; при этом к системе приложены силы
; при этом к системе приложены силы  а также реакции подпятника и подшипника
а также реакции подпятника и подшипника
(рис. 28, б).
Те же внешние силы действуют на систему и в течение промежутка времени от 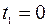 до
до 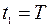 при движении самоходной тележки К.
при движении самоходной тележки К.
Уравнение, выражающее теорему об изменении кинетического момента системы, имеет для этого периода времени вид:
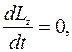 т. е.
т. е. 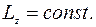
Определим значения кинетических моментов  при
при 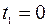 и
и 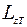 при
при 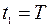 и приравняем эти значения.
и приравняем эти значения.
Для 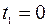
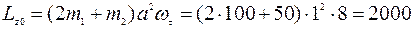 кг·м2/с.
кг·м2/с.
При  >0 скорость точки К складывается из относительной скорости
>0 скорость точки К складывается из относительной скорости 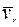 по отношению к пластине H и переносной скорости
по отношению к пластине H и переносной скорости 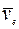 в движении вместе с пластиной. Поэтому для
в движении вместе с пластиной. Поэтому для 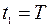 покажем два вектора количества движения точки:
покажем два вектора количества движения точки:  и
и 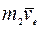 (рис. 28, б).
(рис. 28, б).
В момент времени 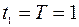 с
с  , тогда центральный угол
, тогда центральный угол 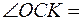
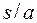
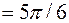 , и точка К попадает в точку B пластины, поэтому
, и точка К попадает в точку B пластины, поэтому
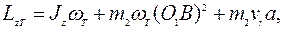 (4)
(4)
где момент инерции 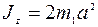 ; расстояние
; расстояние  (как гипотенуза прямоугольного равнобедренного треугольника
(как гипотенуза прямоугольного равнобедренного треугольника 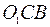 ); относительная скорость
); относительная скорость 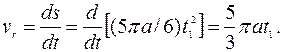
Тогда при 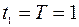 с из выражения (4) получим
с из выражения (4) получим
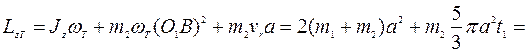
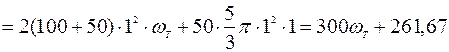 .
.
Приравнивая  и
и 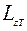 , находим:
, находим:
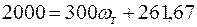 , откуда
, откуда 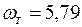 рад/с.
рад/с.
Ответ: 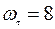 рад/с;
рад/с; 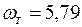 рад/с.
рад/с.
Не нашли, что искали? Воспользуйтесь поиском: