Равновесия механической системы

Схемы находящихся в равновесии механизмов показаны на рис. 54−58, а необходимые данные приведены в табл. 10.

Применяя принцип возможных перемещений и пренебрегая сила­ми сопротивления, определить величину, указанную в предпоследнем столбце табл. 10.

Примечание. Механизмы в вариантах 3, 6, 10, 14, 16, 18, 19, 25 и 30 располо­жены в вертикальной плоскости, а остальные — в горизонтальной.

Пример выполнения задания (рис. 59). Дано: Н, с=100Н/см; см; см; см;

Определить значение момента , уравновешивающего находящийся в горизонтальной плоскости механизм в данном положении, если известно, что пружина растянута на величину 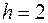см.

Решение. Рассматрива­емый механизм (рис. 59) находится

в равновесии под действием следующих активных силовых факторов: силы и пары сил с моментом , а также сил тяжести звеньев механизма. Силу упругости пружины как реакцию неидеальной связи условно переводим в разряд активных сил и изображаем на расчетной схеме. Остальные наложенные на механизм связи являются идеальными и поэтому их реакции на схеме не показываются.

Составим уравнение работ, выражающее принцип возможных пе­ремещений:

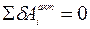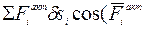
или (1)

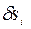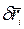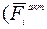
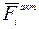где − модуль возможного перемещения точки приложения активной силы ; − угол между векторами и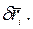

Сообщим рассматриваемой механической системе любое возможное перемещение, допускаемое наложенными на нее связями, например, такое, при котором кривошип ОА совершит поворот вокруг точки О по ходу часовой стрелки на угол . При этом звено АВ повернется на угол вокруг своего мгновенного центра скоростей Р, а звено ВС − на угол вокруг точки . Модули возможных перемещений точек В и С приложения сил и обзначим и . Тогда уравнение работ (1) примет следующий вид:

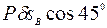
. (2)

При составлении уравнения (2) учтено, что возможные работы сил тяжести звеньев механизма равны нулю, поскольку эти силы перпендикулярны возможным перемещениям их точек приложения.

Для определения момента M в уравнении (2) возможные перемещения и необходимо выразить через . Из рис. 59 яс-но, что ;

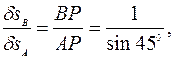
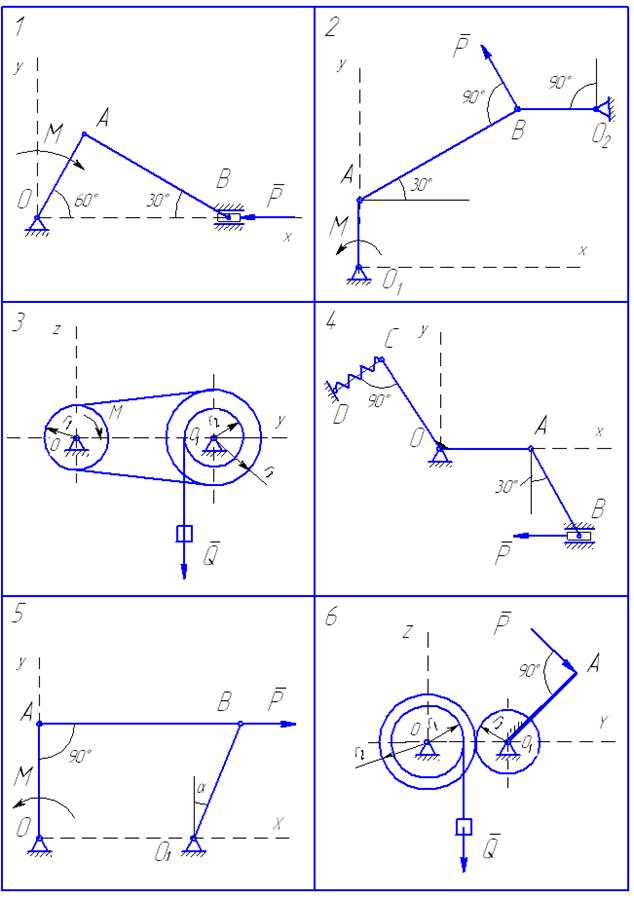Рис. 54

Рис. 55

Рис. 56

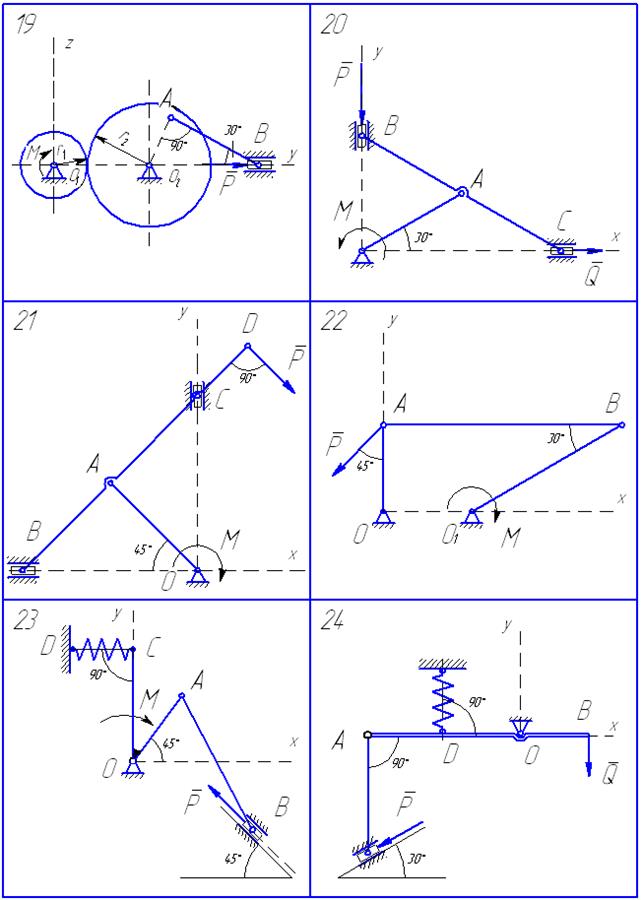Рис. 57

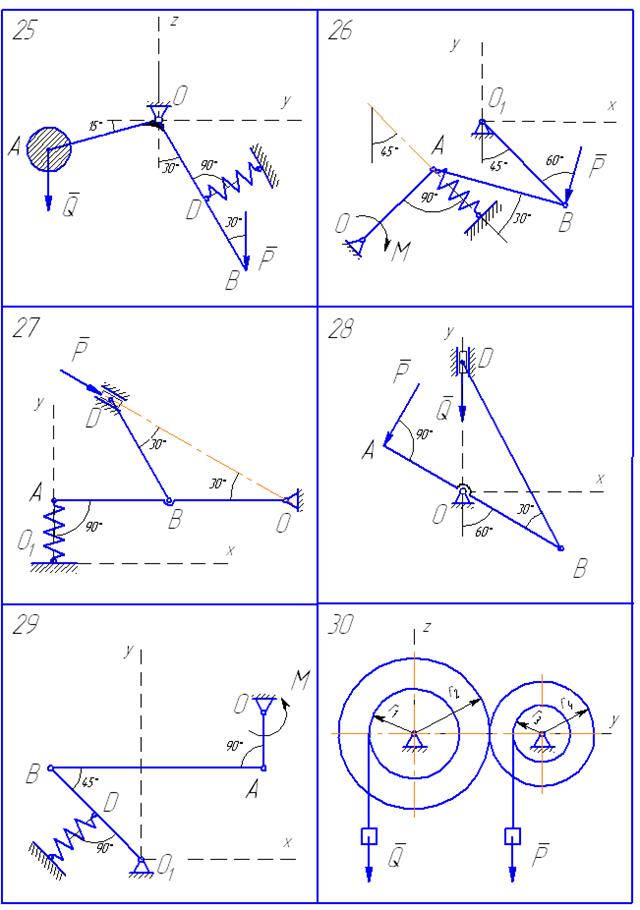
Рис. 58

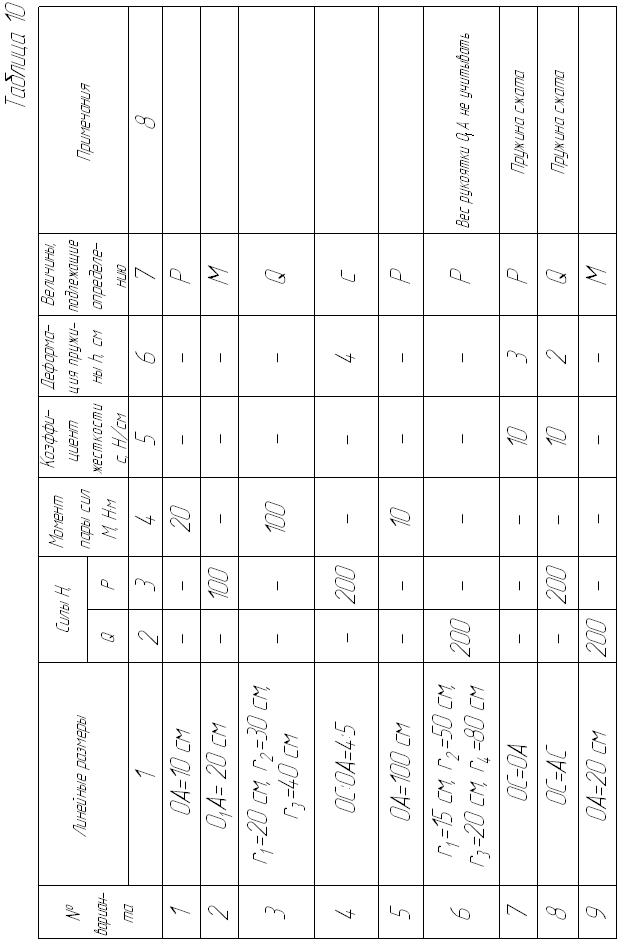
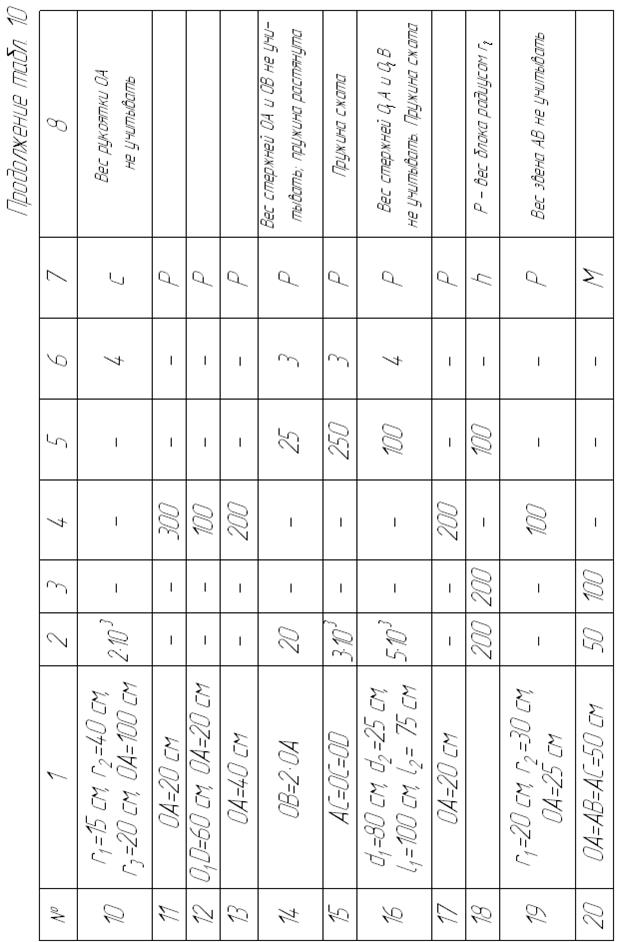
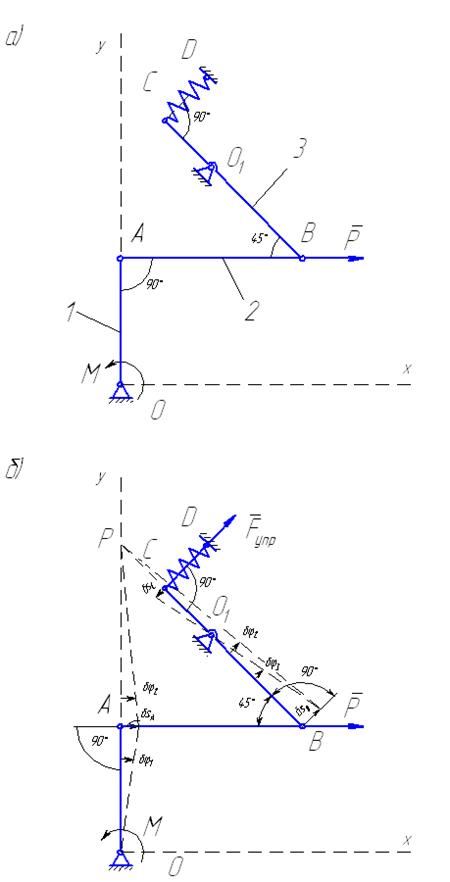
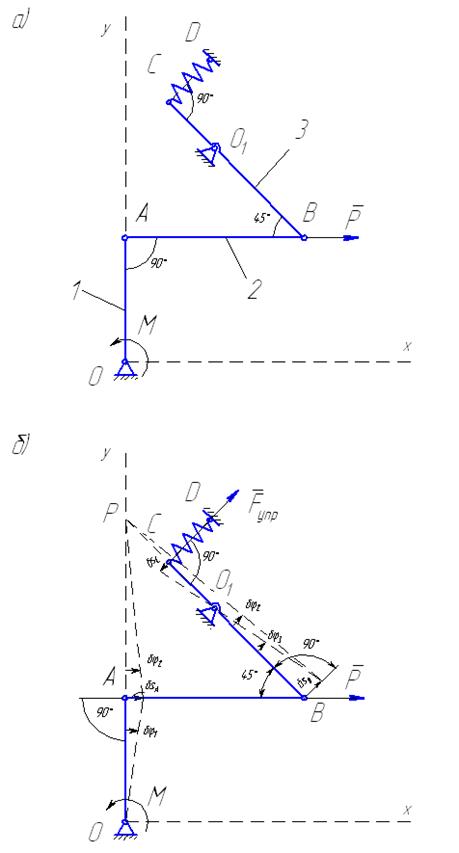
Рис. 59

тогда

.

Так как , то .

Сила упругости пружины пропорциональна ее деформации: 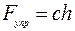. Подставив в уравнение работ (2) выражение силы упругости и выражения для возможных перемещений и , получим:

,

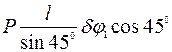
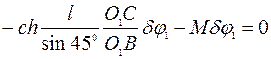откуда

Н·м.

Ответ: кН·м.

ПРИНЦИП ДАЛАМБЕРА – ЛАГРАНЖА
И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ

Не нашли, что искали? Воспользуйтесь поиском: