
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Механической системы. Определить динамические реакции внешних связей механической системы:
Определить динамические реакции внешних связей механической системы:
а) в произвольный момент времени − для вариантов 4, 5, 10, 12−14, 16−18, 21−30 (рис. 47−51);
б) в момент времени 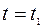 − для вариантов 1, 8, 9, 11, 20;
− для вариантов 1, 8, 9, 11, 20;
в) в тот момент времени, когда угол поворота  − для вариантов 2, 3, 6, 7;
− для вариантов 2, 3, 6, 7;
г) в положении, показанном на чертеже, − для вариантов 15 и 19.
На схемах (рис. 47−51) плоскость хОу (хАу) горизонтальна, плоскость yOz (yAz) вертикальна. Необходимые длярешения данные приведены в табл. 9, в которой 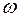 − угловая скорость,
− угловая скорость,  и
и 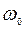 − угол поворота и угловая скорость в начальный момент времени.
− угол поворота и угловая скорость в начальный момент времени.
Поскольку в предлагаемых вариантах задания рассматриваются случаи как равномерного, так и неравномерного вращения системы, приведем примеры выполнения задания для таких случаев.
Пример 1 выполнения задания (рис. 52). Дано:  кг;
кг;  м,
м,  ;
;  ;
;  рад/с.
рад/с.
Найти динамическую реакцию шарнира О вращающегося диска в момент времени, соответствующий повороту диска на угол  .
.
Решение. Рассмотрим диск, вращающийся вокруг горизонтальной неподвижной оси 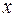 , как объект исследования, на который действуют следующие внешние силы: сила тяжести
, как объект исследования, на который действуют следующие внешние силы: сила тяжести 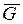 и составляющие
и составляющие  искомой реакции шарнира О. Для определения реакции шарнира воспользуемся принципом Даламбера и добавим к внешним силам, приложенным к диску, силы инерции, которые приведем к центру масс С.
искомой реакции шарнира О. Для определения реакции шарнира воспользуемся принципом Даламбера и добавим к внешним силам, приложенным к диску, силы инерции, которые приведем к центру масс С.
Силы инерции диска, как тела, вращающегося вокруг непод-

 Рис. 47
Рис. 47
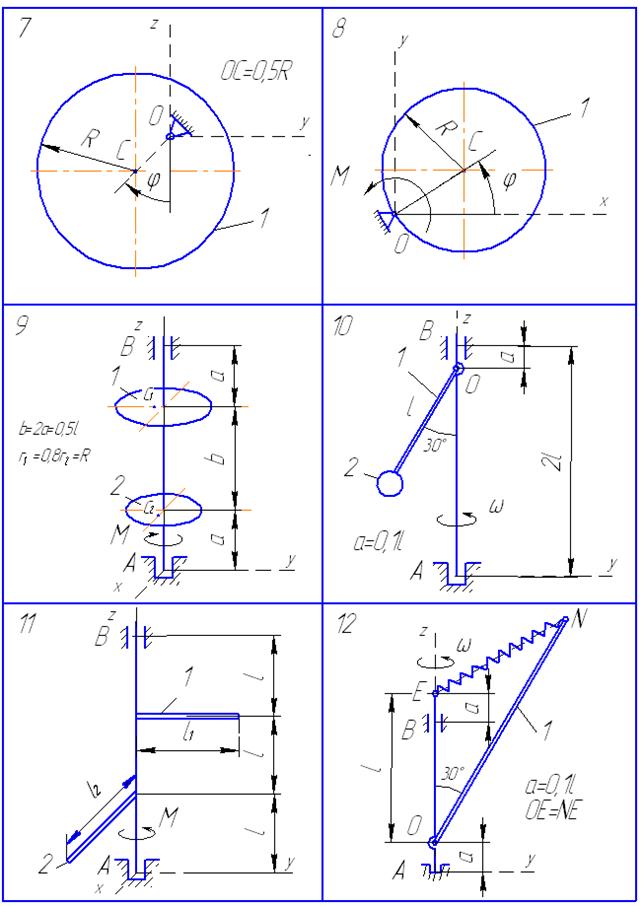
 Рис. 48
Рис. 48

 Рис. 49
Рис. 49
 Рис. 50
Рис. 50

 Рис. 51
Рис. 51


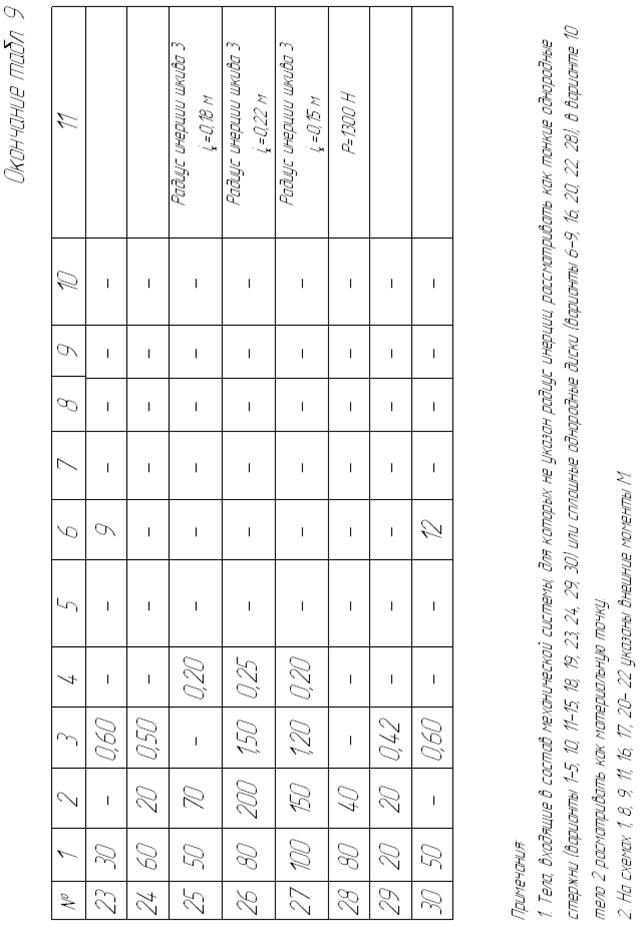

Рис. 52
вижной оси, перпендикулярной его плоскости материальной симмет-
рии и не проходящей через центр масс С, приводятся к главному вектору  , приложенному в центре масс С, и главному моменту
, приложенному в центре масс С, и главному моменту
 относительно центральной оси, параллельной оси вращения.
относительно центральной оси, параллельной оси вращения.
Главный вектор сил инерции вращающегося диска определяется
поформуле
 ,
,
где m − масса диска, а  − ускорение его центра масс С.
− ускорение его центра масс С.
Главный вектор  сил инерции целесообразно представить в виде следующей геометрической суммы:
сил инерции целесообразно представить в виде следующей геометрической суммы:
 ,
,
где  − центробежная составляющая главного вектора
− центробежная составляющая главного вектора  сил инерции, которая направлена противоположно центростремительному ускорению
сил инерции, которая направлена противоположно центростремительному ускорению  и модуль которой определяется по формуле
и модуль которой определяется по формуле
 ; (1)
; (1)
 − вращательная составляющая главного вектора
− вращательная составляющая главного вектора  сил инерции, направленная противоположно вращательному ускорению
сил инерции, направленная противоположно вращательному ускорению  и модуль которой определяется по формуле
и модуль которой определяется по формуле
 . (2)
. (2)
При этом угловое ускорение  направляем в соответствии с направлением момента силы тяжести
направляем в соответствии с направлением момента силы тяжести 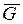 диска относительно оси вращения.
диска относительно оси вращения.
Главный момент  сил инерции направлен противоположно угловому ускорению
сил инерции направлен противоположно угловому ускорению  диска и по модулю равен
диска и по модулю равен
 .
.
Здесь  − момент инерции диска относительно центральной оси, параллельной оси вращения.
− момент инерции диска относительно центральной оси, параллельной оси вращения.
Следовательно,
 . (3)
. (3)
Внешние силы и силы инерции диска составляют плоскую систему сил и должны удовлетворять следующим трем кинетостатическим уравнениям, вытекающим из принципа Даламбера:
 ;
;  (4)
(4)
 ;
;  (5)
(5)
 .
.  . (6)
. (6)
Подставляя в последнее уравнение выражения (2) и (3), получим
 .
.
Отсюда определяем угловое ускорение  :
:
 . (7)
. (7)
Для определения угловой скорости 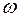 диска, учтя противоположность направлений
диска, учтя противоположность направлений 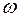 и
и  (рис. 58, б), представим выражение (7) в виде
(рис. 58, б), представим выражение (7) в виде
 .
.
Далее, умножив левую и правую части этого уравнения на дифференциал  :
:
 ,
,
перейдем к переменным 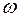 и
и  :
:
 . (8)
. (8)
Интегрируя дифференциальное уравнение (8) в заданных пределах, получим:
 , откуда
, откуда  и
и
 . (9)
. (9)
При найденных значениях  и
и  из равенств (1) и (2) для
из равенств (1) и (2) для  получим
получим

 Н;
Н;
 Н.
Н.
Тогда для момента времени, соответствующего повороту диска на угол  , при заданных исходных данных из кинетостатических
, при заданных исходных данных из кинетостатических
уравнений (4) и (5) определим искомые динамические реакции:

 Н;
Н;

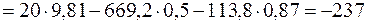 Н.
Н.
Ответ: 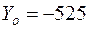 Н;
Н;  Н.
Н.
Пример 2 выполнения задания. Дано:  кг;
кг;  кг;
кг;  рад/с
рад/с  ;
; 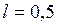 м;
м;  . Схема системы и необходимые размеры приведены на рис. 53, а. Найти динамические реакции подпятника А и подшипника В, а также пружины KD. Поперечными размерами однородного ломаного стержня
. Схема системы и необходимые размеры приведены на рис. 53, а. Найти динамические реакции подпятника А и подшипника В, а также пружины KD. Поперечными размерами однородного ломаного стержня  и массой пружины пренебречь.
и массой пружины пренебречь.
Решение. Рассматриваемая механическая система, состоящая из ломаного стержня  и невесомого вертикального вала, равномерно вращается вокруг неподвижной оси
и невесомого вертикального вала, равномерно вращается вокруг неподвижной оси 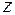 . Система находится под действием следующих внешних сил: сил тяжести
. Система находится под действием следующих внешних сил: сил тяжести 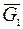 ,
, 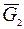 частей 1 и 2 стержня, составляющих
частей 1 и 2 стержня, составляющих  реакции подпятника А и реакции
реакции подпятника А и реакции  подшипника В.
подшипника В.
Для определения реакций подшипника и подпятника воспользуемся принципом Даламбера, добавив к внешним силам силы инерции частей стержня и составив соответствующие кинетостатические уравнения.
Приведем силы инерции частей стержня, равномерно вращающегося вокруг вертикальной неподвижной оси 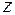 , к простейшему виду. Для этого рассмотрим элементарную массу
, к простейшему виду. Для этого рассмотрим элементарную массу  длины
длины  части 1 стержня (рис. 53, в). Сила инерции
части 1 стержня (рис. 53, в). Сила инерции  элементарной массы
элементарной массы 
 направлена противоположно ее ускорению
направлена противоположно ее ускорению  Поскольку при равномерном вращении стержня это ускорение является центростремительным, сила инерции
Поскольку при равномерном вращении стержня это ускорение является центростремительным, сила инерции  направлена по горизонтали от оси вращения. Модуль этой силы инерции
направлена по горизонтали от оси вращения. Модуль этой силы инерции
 .
.
Так как стержень является однородным, то  ,
,
где  − масса единицы длины стержня, и тогда
− масса единицы длины стержня, и тогда
 .
.
Таким образом, силы инерции точек части 1 стержня представляют собой систему параллельных сил, которая приводится к равнодействующей  , равной их главному вектору
, равной их главному вектору  и, следовательно,
и, следовательно,
 ,
,
где  − ускорение центра масс
− ускорение центра масс 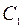 этой части стержня:
этой части стержня:
 .
.
Тогда модуль равнодействующей сил инерции 
 .
.
Линию действия равнодействующей  можно определить, найдя зависимость интенсивности
можно определить, найдя зависимость интенсивности  этих сил от текущей координаты
этих сил от текущей координаты 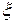 элементарной длины
элементарной длины  рассматриваемой части стержня, и построив эпюру
рассматриваемой части стержня, и построив эпюру 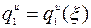 .
.
При этом  , т. е. интенсивность
, т. е. интенсивность  пропорциональна координате
пропорциональна координате 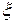 и, следовательно, эпюра распределенных сил инерции представляет собой треугольник, а линия действия равнодействующей
и, следовательно, эпюра распределенных сил инерции представляет собой треугольник, а линия действия равнодействующей  параллельна этим силам и проходит через центр тяжести площади эпюры на расстоянии
параллельна этим силам и проходит через центр тяжести площади эпюры на расстоянии  от точки О (рис. 53, б).
от точки О (рис. 53, б).
Силы инерции вертикальной части 2 стержня, совершающей криволинейное поступательное движение, приводятся к равнодействующей  , которая определяется аналогично
, которая определяется аналогично  :
:
 ;
;
модуль этой равнодействующей


Рис. 53
Интенсивность  распределенных сил инерции части 2 стержня
распределенных сил инерции части 2 стержня
 ,
,
поэтому эпюра этих сил представляет собой прямоугольник, а линия действия их равнодействующей  проходит через центр тяжести площади этой эпюры, и, следовательно, через центр масс
проходит через центр тяжести площади этой эпюры, и, следовательно, через центр масс  рассматриваемой части стержня (рис. 53, б).
рассматриваемой части стержня (рис. 53, б).
Приложенные внешние силы и силы инерции образуют плоскую уравновешенную систему сил. Составляя для этой системы сил согласно принципу Даламбера три уравнения равновесия, получим:
 ;
;  (10)
(10)
 ;
;  (11)
(11)
 ;
;  . (12)
. (12)
С учетом исходных данных находим
 Н;
Н;
 Н;
Н;
 м;
м;
 м;
м;
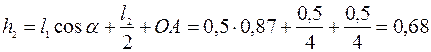 м;
м;
 м
м
Из уравнения (12) получим


 Н
Н  кН.
кН.
Тогда из уравнений (10) и (11) следует
 Н
Н  кН.
кН.
 Н
Н  кН.
кН.
Для определения силы упругости  пружины в качестве объекта исследования рассмотрим ломаный стержень
пружины в качестве объекта исследования рассмотрим ломаный стержень  , к которому приложены следующие внешние силы: силы тяжести
, к которому приложены следующие внешние силы: силы тяжести 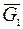 ,
, 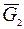 частей 1 и 2 стержня, составляющие
частей 1 и 2 стержня, составляющие  реакции шарнира О, силы инерции
реакции шарнира О, силы инерции  и
и  , а также искомая сила упругости
, а также искомая сила упругости  растянутой пружины (рис. 53, г). На основании принципа Даламбера составим уравнение моментов перечисленных сил относительно точки О:
растянутой пружины (рис. 53, г). На основании принципа Даламбера составим уравнение моментов перечисленных сил относительно точки О:

 ,
,
где  .
.
Отсюда


 Н
Н  кН.
кН.
Ответ:  кН;
кН;  кН;
кН;  кН;
кН;  кН.
кН.
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
И ОБЩЕЕ УРАВНЕНИЕ СТАТИКИ
Не нашли, что искали? Воспользуйтесь поиском: