Механической системы

Механическая система под действием сил тяжести приходит в дви­жение из состояния покоя; начальное положение системы показано на рис. 29 − 33. Учитывая трение скольжения тела 1 (варианты 1 − 3, 5, 6, 8 − 12, 17 − 23, 28 − 30) и сопротивление качению тела 3, катящегося без скольжения (варианты 2, 4, 6 − 9, 11, 13 − 15, 20, 21, 24, 27, 29), пренебрегая другими силами сопротивления и мас­сами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s.

В задании приняты следующие обозначения: m ₁, m ₂, m ₃, m ₄ − массы тел 1, 2, 3, 4; R ₂, r ₂, R ₃, r ₃ − радиусы больших и малых окружностей колес; i _{2 x}, i _{3 ξ} – радиусы инерции тел 2 и 3 относительно горизонтальных осей, проходящих через их центры масс; α, β − углы наклона плоскостей к горизонту; f − коэффициент трения сколь­жения;

δ − коэффициент трения качения.

Необходимые для решения данные приведены в табл. 6. Блоки и катки, для которых радиусы инерции в таблице не указаны, счи­тать сплошными однородными дисками. В вариантах 17, 26 и 28 шатун 3 рассматривать как тонкий однородный стержень.

Наклонные участки нитей параллельны соответствующим наклон­ным плоскостям.

Пример выполнения задания (рис. 34). Дано: − масса груза 1, 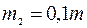, , , r₂ = R₃ = 10 см, α = 60°, f = 0,1, s = 0,05π м. Массой кривошипа (водила) ОС пренебречь. На рис. 34, а показана механическая система в начальном положении.

Найти 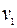– скорость груза 1 в положении, соответствующем его перемещению на заданное расстояние .

Решение. Объект исследования – механическая система связанных тел: груз 1, канат, колесо 2 и сателлитный механизм, состоящий

Рис. 29

Рис. 30

Рис. 31

Рис. 32

Рис. 33

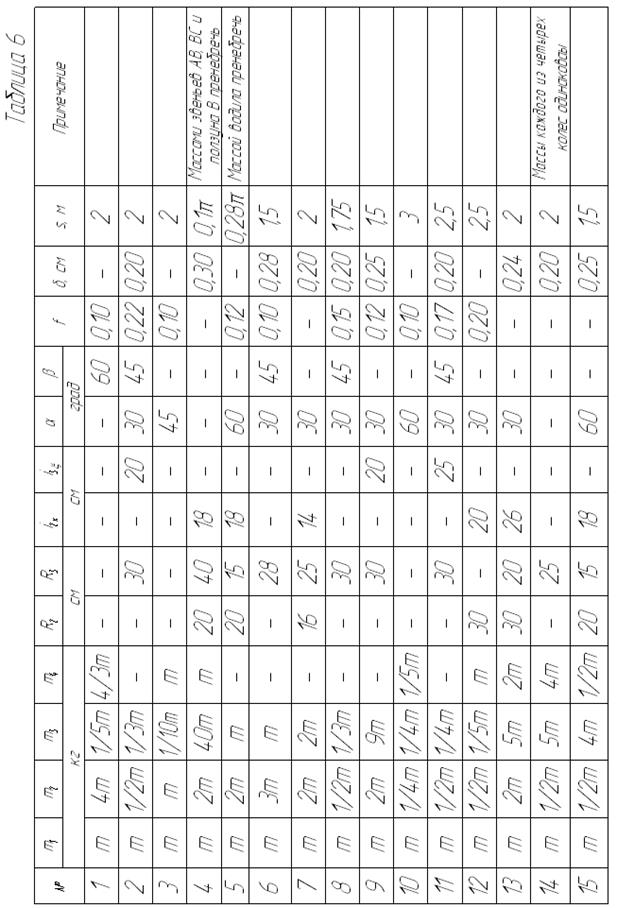
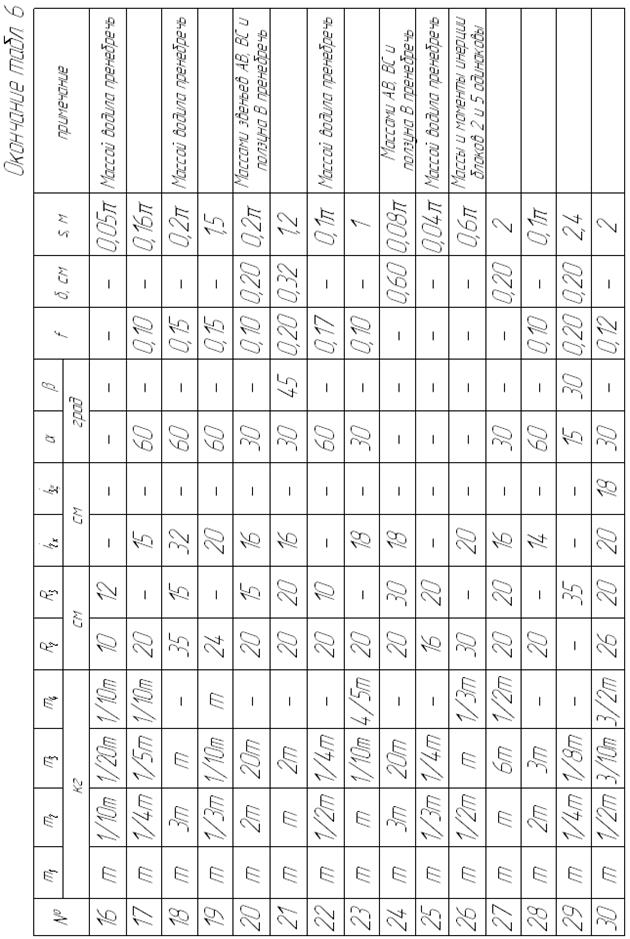
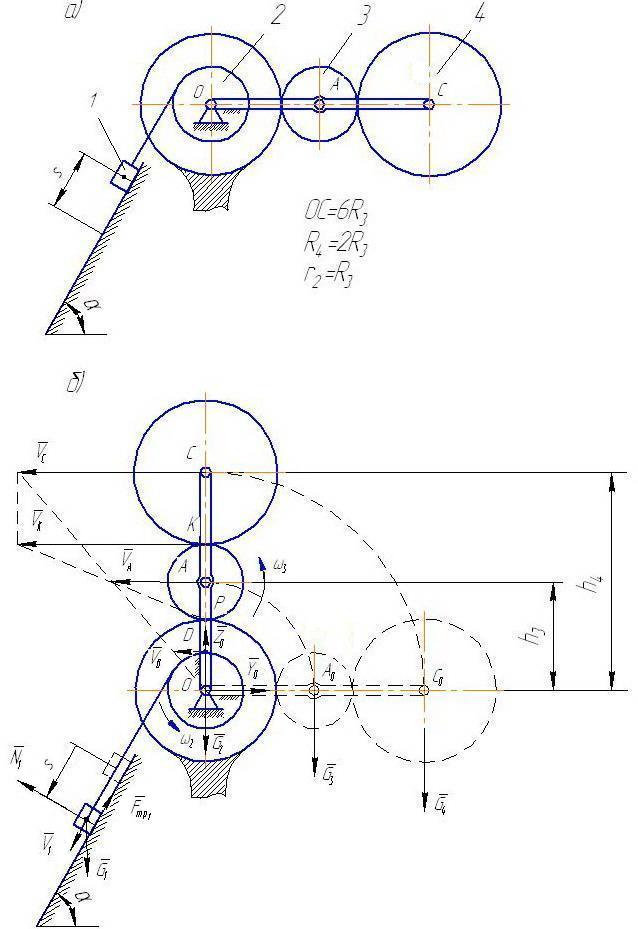Рис. 34

из кривошипа ОС, неподвижного колеса и колес 3, 4 с подвижными осями. Применим теорему об изменении кинетической энер­гии системы:

,

(1)

где и Т — кинетическая энергия системы в начальном и конеч­ном

положениях; и − сумма работ всех внешних и внутренних сил, приложенных к системе, на соответствующих перемещениях их точек приложения.

Для рассматриваемой системы, состоящей из абсолютно твердых тел, связанных нерастяжимым канатом,

.

В начальном положении система находится в покое, поэтому Т ₀ = 0. Следовательно, уравнение (1) принимает вид:

.

(2)

Выразим кинетическую энергию рассматриваемой системы через искомую скорость 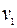груза 1, а сумму работ внешних сил, приложенных к системе, − через его заданное перемещение .

Кинетическая энергия системы Т в конечном ее положении (рис. 34, б)равна сумме кинетических энергий тел 1, 2,3, 4:

. (3)

Кинетическая энергия поступательно движущегося груза 1

. (4)

Кинетическая энергия колеса 2, вращающегося вокруг непод­вижной оси Ох,

, (5)

где 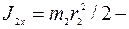момент инерции колеса 2 относительно его центральной оси 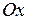; − угловая скорость колеса 2.

Скорость точки D колеса 2 равна скорости 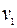груза 1, поскольку нить, соединяющая груз и колесо, является нерастяжимой и не скользит по ободу колеса.

Тогда , 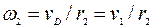и выражение для кинетической энергии колеса 2 примет вид:

. (6)

Кинетическая энергия колеса 3, совершающего плоское движение,

, (7)

где скорость центра масс колеса 3; момент инерции колеса относительно его центральной оси как сплошного однородного диска; угловая скорость колеса.

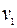Выразим величины и через скорость . Центр масс колеса 3 совпадает с точкой А кривошипа ОС, жестко связанного с колесом 2 и вращающегося с угловой скоростью , поэтому

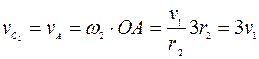. (8)

Так как колесо 3 катится без скольжения по неподвижному контуру, то мгновенный центр скоростей этого колеса находится в точке Р контакта с контуром,следовательно,

. (9)

После подстановки (8) и (9) в выражение (7) получим

.

Таким образом,

. (10)

Для определения кинетической энергии колеса 4 найдем скорость центра масс и угловую скорость этого колеса.

Центр масс колеса 4 совпадает с точкой С кривошипа ОС,

поэтому скорость этого центра равна

. (11)

При этом вектор направлен перпендикулярно кривошипу OC в соответствии с круговой стрелкой .

Скорость точки К контакта колеса 4 с колесом 3

,

то есть по модулю равна скорости и направлена так же, как и вектор . Таким образом, векторы скоростей двух точек и колеса 4, совершающего движение в плоскости, геометрически равны: , откуда следует, что угловая скорость колеса , т. е. оно совершает криволинейное поступательное движение.

Тогда кинетическая энергия колеса 4

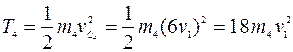. (12)

Кинетическая энергия всей механической системы определяется по формуле (3) с учетом выражений (4), (6), (10), (12)

.

Подставляя сюда заданные значения масс, получаем:

. (13)

Найдем сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении. Покажем приложенные к сис­теме внешние силы: силы тяжести груза и колес, нормальную реакцию наклонной плоскости, силу трения скольжения и составляющие , реакции опоры О (рис. 34, б).

Работа силы тяжести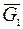

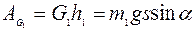. (14)

Работа нормальной реакции как силы, перпендикулярной перемещению точки ее приложения, равна нулю.

Работа силы трения скольжения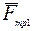

.

Так как

то

. (15)

Работа сил , точка О приложения которых является неподвижной, равна нулю.

Для определения работ сил и найдем угол поворота кривошипа ОС, соответствующий перемещению груза 1. Для этого

выражение для угловой скорости 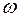кривошипа

,

с учетом того, что и , приведем к виду

,

откуда получим

.

После интегрирования при нулевых начальных условиях

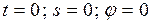() найдем, что

.

При перемещении груза 1 по наклонной плоскости на расстояние кривошип ОС повернется на угол

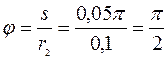
и переместится из начального горизонтального положения в вертикальное , а точки А и С приложения сил тяжести и совершат вертикальное перемещение соответственно на высоту

и

.

Работы сил тяжести и при этом составят:

, (16)

. (17)

Сумма работ внешних сил определится сложением работ, вычисленных по формулам (14) − (17):

.

Подставляя исходные данные, получим:

. (18)

Согласно выражению (2) приравняем значения Т и , определяемые по формулам (13) и (18):

,

откуда

м/с.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ

ТВЕРДОГО ТЕЛА

Не нашли, что искали? Воспользуйтесь поиском: