
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задание Д-9. Исследование плоского движения
Твердого тела
Определить максимальную величину постоянной силы  , под действием которой колесо массой
, под действием которой колесо массой 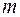 катится без скольжения по неподвижной опорной плоскости. Найти также для этого случая уравнение движения центра масс C колеса,если в начальный момент времени координата искорость центра С равны нулю (
катится без скольжения по неподвижной опорной плоскости. Найти также для этого случая уравнение движения центра масс C колеса,если в начальный момент времени координата искорость центра С равны нулю (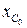 = 0;
= 0;  ). Варианты задания показаны на рис. 41−45, а необходимые для решения данные приведены в табл. 8.
). Варианты задания показаны на рис. 41−45, а необходимые для решения данные приведены в табл. 8.
В задании приняты следующие обозначения: 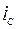 − радиус инерции колеса относительно центральной оси, перпендикулярной к его плоскости; R и r − радиусы большой ималой окружностей колеса;
− радиус инерции колеса относительно центральной оси, перпендикулярной к его плоскости; R и r − радиусы большой ималой окружностей колеса;
 − коэффициент сцепления; δ −
− коэффициент сцепления; δ −  коэффициент трения качения.
коэффициент трения качения.
Колеса, для которых радиусы инерции не указаны, считать сплошными однородными дисками.
Пример выполнения задания (рис. 46). Дано: т= 250 кг;
R = 50 см; r = 25 см; 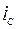 = 40 см; α= 20°; β= 30°;
= 40 см; α= 20°; β= 30°;  = 0,25; δ = 0,012 м (рис. 46, а).
= 0,25; δ = 0,012 м (рис. 46, а).
Решение. Колесо, являющееся объектом исследования, совершает плоское движение, находясь под действием силы тяжести 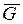 ,нормальной реакции
,нормальной реакции  опорной плоскости, силы
опорной плоскости, силы  , силы сцепления
, силы сцепления 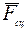 и момента трения качения
и момента трения качения 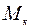 (рис. 46, б).
(рис. 46, б).
При составлении дифференциальных уравнений движения колеса следует считать моменты сил и пар сил положительными, если они способствуют вращению колеса. Силу сцепления 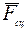 , когда не ясно, куда она направлена, можно направлять в любую сторону. Действительное направление этой силы устанавливается в процессе решения задачи.
, когда не ясно, куда она направлена, можно направлять в любую сторону. Действительное направление этой силы устанавливается в процессе решения задачи.
Дифференциальные уравнения плоского движения колеса составляются в форме

Рис. 41
 Рис. 42
Рис. 42

Рис. 43
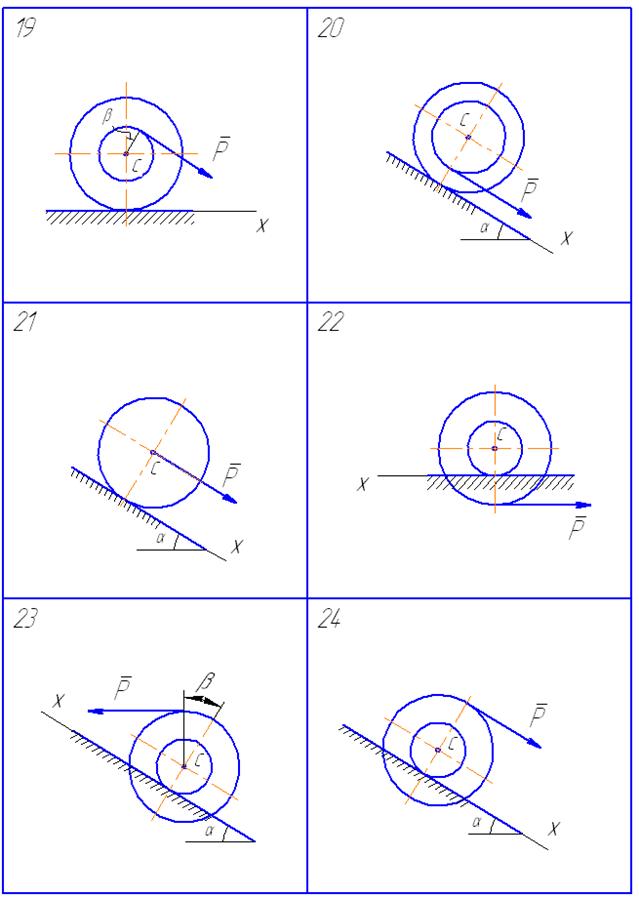 Рис. 44
Рис. 44

Рис. 45
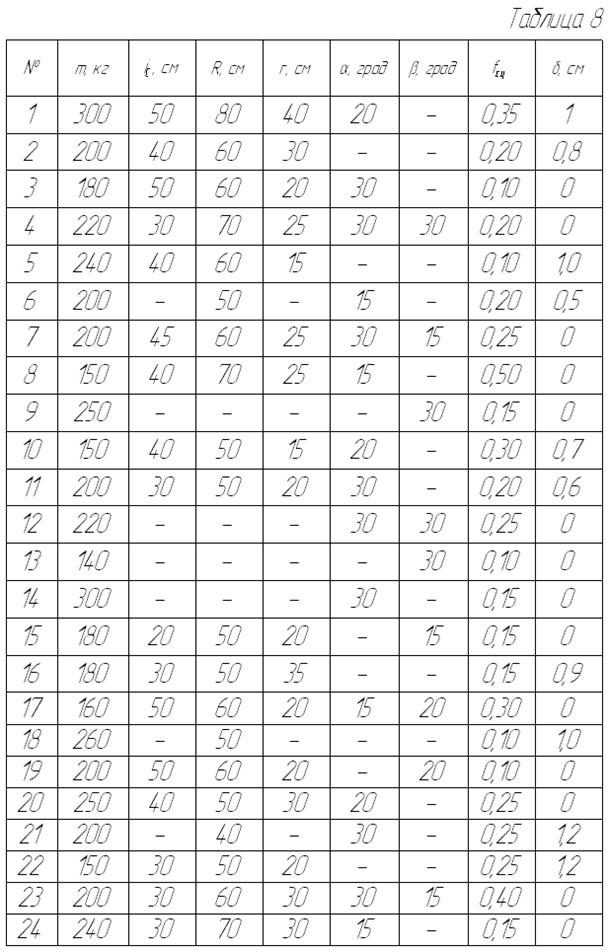

и в рассматриваемом случае имеют вид:
 ; (1)
; (1)
 ; (2)
; (2)
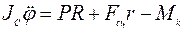 . (3)
. (3)
За положительное направление для моментов принято направление по ходу часовой стрелки, т. е. в ту сторону, куда будет вращаться колесо при движении центра С от оси 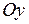 .
.
Поскольку ясно, что 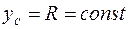 и
и  , то из уравнения (2) получим
, то из уравнения (2) получим
 .
.
Момент трения качения, действующий со стороны опорной плоскости, определяется следующим образом:
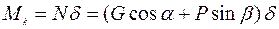 .
.
Поэтому уравнения (1) и (3) содержат четыре неизвестные величины (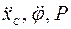 и
и  ), и, следовательно, необходимо найти еще одно
), и, следовательно, необходимо найти еще одно
соотношение, связывающее эти величины. Для этого учтем, что 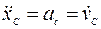 (так как центр C движется прямолинейно) и что при качении без скольжения в точке К находится мгновенный центр скоростей колеса.
(так как центр C движется прямолинейно) и что при качении без скольжения в точке К находится мгновенный центр скоростей колеса.
Тогда угловая скорость колеса 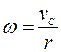 , а его угловое ускорение
, а его угловое ускорение 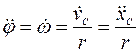 . При этом уравнение (3) принимает следующий
. При этом уравнение (3) принимает следующий
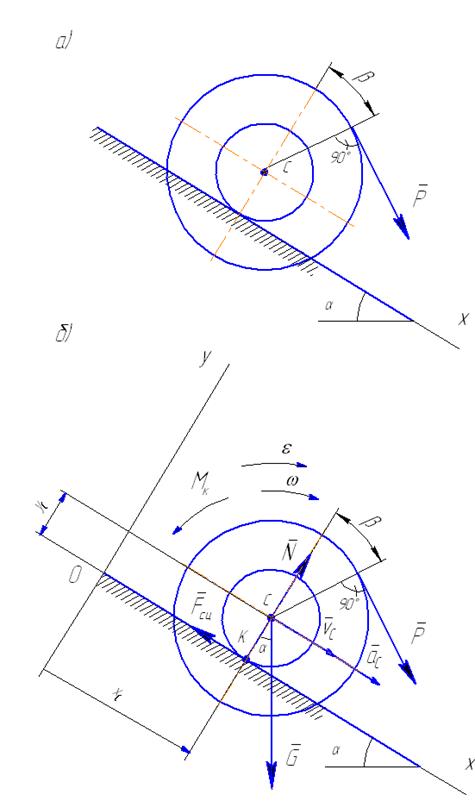
Рис. 46
вид
 (4)
(4)
Для исключения  разделим уравнение (1) на (4):
разделим уравнение (1) на (4):
 ,
,
откуда
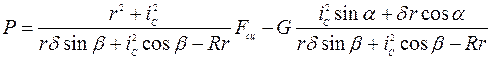 . (5)
. (5)
Заметим, что выражение (5) дает возможность судить о правильности выбранного направления силы сцепления. Приближение силы P к своему предельному значению (искомой величине) сопровождается, естественно, возрастанием силы сцепления. Поэтому в выражении (5), приведенном к виду 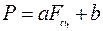 , коэффициент a должен быть положительным. В нашем случае
, коэффициент a должен быть положительным. В нашем случае
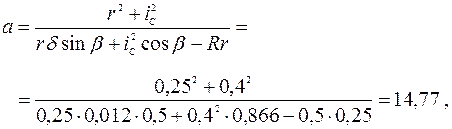
т. е. направление силы сцепления 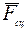 на расчетной схеме указано верно.
на расчетной схеме указано верно.
В противном случае следует изменить направление 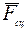 на противоположное и внести соответствующие изменения в дифференциальные уравнения (1) − (3).
на противоположное и внести соответствующие изменения в дифференциальные уравнения (1) − (3).
Максимальное значение силы сцепления:
 ).
).
Подставляя максимальное значение  в уравнение (5), найдем максимальное значение силы
в уравнение (5), найдем максимальное значение силы  , при действии которой колесо катится без скольжения:
, при действии которой колесо катится без скольжения:

или
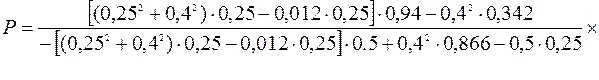
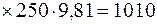 Н.
Н.
Сила сцепления
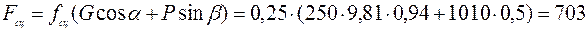 Н.
Н.
Дифференциальное уравнение движения центра колеса

или
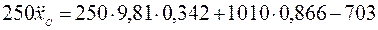 ,
,
откуда
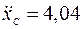 м/с2.
м/с2.
Дважды интегрируя это дифференциальное уравнение, находим:
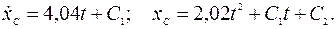
Подставляя начальные условия ( ;
; 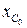 = 0;
= 0; 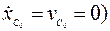 в полученные уравнения, определяем значения постоянных интегрирования:
в полученные уравнения, определяем значения постоянных интегрирования:
 и
и 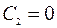 .
.
Следовательно, уравнение движения центра колеса
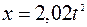 (м).
(м).
Ответ: 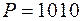 Н;
Н; 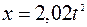 (м).
(м).
Не нашли, что искали? Воспользуйтесь поиском: