
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Механической системы с одной степенью свободы
Для заданной механической системы с помощью общего уравнения динамики определить ускорения грузов и центров масс катков, а также силы натяжения нитей, к которым прикреплены эти элементы системы. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя.
Варианты механических систем показаны на рис. 60−64, а

Рис. 60
 Рис. 61
Рис. 61
 Рис. 62
Рис. 62
 Рис. 63
Рис. 63
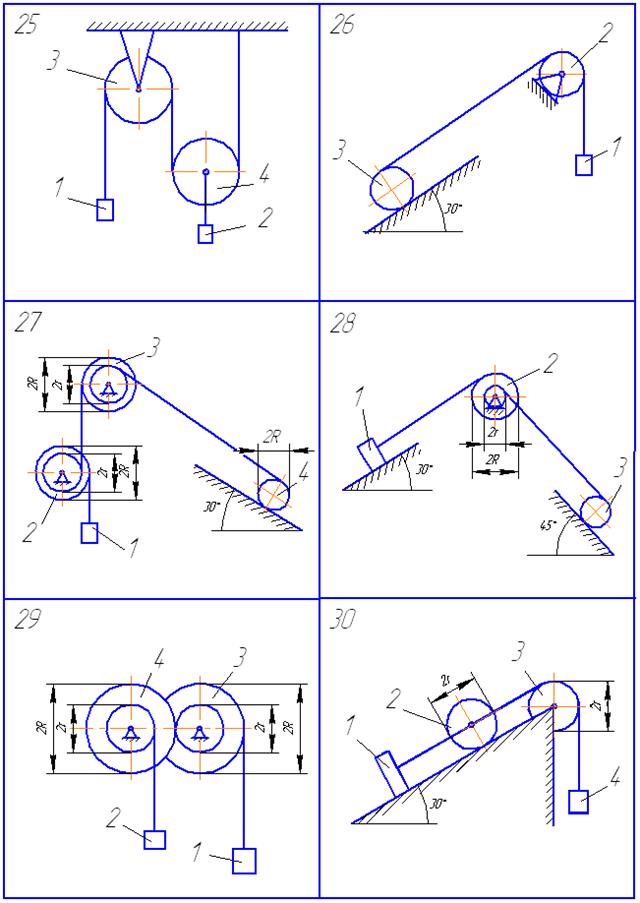 Рис. 64
Рис. 64



необходимые для решения данные приведены в табл. 11.
Блоки и катки, для которых радиусы инерции в таблице не
указаны, считать сплошными однородными цилиндрами.Все катки, включая и катки, обмотанные нитями, перемещаются по опорным поверхностям без скольжения.
Пример выполнения задания (рис. 65). Дано: 
 радиус инерции барабана 2 относительно неподвижной оси вращения
радиус инерции барабана 2 относительно неподвижной оси вращения 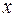 ;
;  Определить ускорения гру-
Определить ускорения гру-
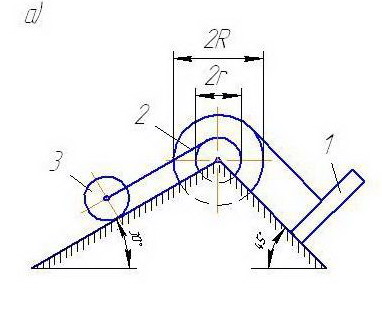

Рис. 65
за 1 и центра масс катка 3, а такжесилы натяжения ветвей 1 −2 и 2−3 нитей.
Решение. В качестве объекта исследования рассмотрим движущуюся механическую систему, состоящую из груза 1, барабана 2 и катка 3. Для определения искомых ускорений на основании принципа Даламбера – Лагранжа составим общее уравнение динамики рассматриваемой системы. Система приходит в движение из состояния покоя, поэтому направления ускорений тел соответствуют направлениям их движения.
Положим, что при движении системы груз 1 опускается вниз по наклонной плоскости (рис. 65).
На механическую систему действуют следующие активные силы: силы тяжести 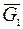 −груза 1,
−груза 1, 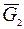 − барабана 2,
− барабана 2, 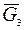 − катка 3.
− катка 3.
Ввиду того, что среди связей, наложенных на систему имеется неидеальная (шероховатая наклонная плоскость, по которой скользит груз), при составлении общего уравнения динамики ее реакция – сила трения скольжения  учитывается наряду с активными силами системы. При этом необходимо правильно показать направление силы трения.
учитывается наряду с активными силами системы. При этом необходимо правильно показать направление силы трения.
Если в результате решения задачи искомое ускорение получается отрицательным, значит, в рассматриваемом случае направление движения системы выбрано ошибочно и поэтому расчет необходимо повторить, изменив направление силы трения и внеся соответствующие поправки в общее уравнение динамики.
В соответствии с принципом Даламбера – Лагранжа реакции идеальных связей системы не учитываются и на расчетной схеме не показываются.
Добавим к действующим на систему силам силы инерции элементов системы, приведя их к простейшему виду. Силы инерции груза 1, движущегося поступательно с ускорением  , приводятся к равнодействующей
, приводятся к равнодействующей  , направленной противоположно этому ускорению и приложенной в центре масс груза. Силы инерции барабана 2, вращающегося вокруг неподвижной оси с угловым ускорением
, направленной противоположно этому ускорению и приложенной в центре масс груза. Силы инерции барабана 2, вращающегося вокруг неподвижной оси с угловым ускорением  , приводятся к паре с моментом
, приводятся к паре с моментом  , направленным в сторону, противоположную этому угловому ускорению. Силы инерции катка 3, совершающего плоское движение, приводятся к главному вектору
, направленным в сторону, противоположную этому угловому ускорению. Силы инерции катка 3, совершающего плоское движение, приводятся к главному вектору  , направленному противоположно ускорению
, направленному противоположно ускорению  центра масс катка и приложенному в этом центре, и главному моменту
центра масс катка и приложенному в этом центре, и главному моменту  относительно центральной оси катка, направленному в сторону, противоположную угловому ускорению
относительно центральной оси катка, направленному в сторону, противоположную угловому ускорению 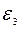 катка.
катка.
Для определения ускорения  груза 1 применим общее уравнение динамики:
груза 1 применим общее уравнение динамики:
 , (1) где
, (1) где  − сумма элементарных работ активных сил;
− сумма элементарных работ активных сил;
 − сумма элементарных работ сил инерции.
− сумма элементарных работ сил инерции.
Зафиксировав систему в текущем положении и сообщив ей возможное перемещение, допускаемое связями (рис. 65, б), составим уравнение (1):
 (2)
(2)
где  и
и  − возможные перемещения груза и центра масс катка;
− возможные перемещения груза и центра масс катка;
 и
и  − углы поворотов барабана и катка.
− углы поворотов барабана и катка.
Поскольку зависимости между возможными перемещениями такие же, как и между соответствующими скоростями, выразим скорость центра масс катка и угловые скорости барабана и катка через скорость груза:
 ;
;  ;
;
Так как каток катится без скольжения, то точка его контакта с неподвижной наклонной плоскостью является мгновенным центром скоростей катка и поэтому
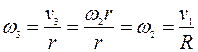 .
.
Аналогичные зависимости имеют место и между возможными перемещениями:
 (3)
(3)
Теперь, дифференцируя полученные выше соотношения, связывающие  ,
,  и
и  со скоростью
со скоростью 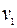 , получим зависимости между угловыми ускорениями
, получим зависимости между угловыми ускорениями  и
и 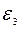 барабана и катка, а также ускорением
барабана и катка, а также ускорением  центра масс катка и искомым ускорением
центра масс катка и искомым ускорением  груза:
груза:
 . (4)
. (4)
Уравнение (2) с учетом соотношений (3) принимает вид
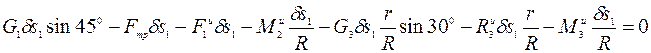
или, сокращая на  , получим:
, получим:
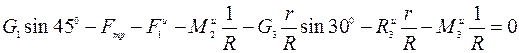 . (5)
. (5)
Учитывая соотношения (4) и исходные данные задачи
 ,
,
вычислим модули сил инерции  ,
,  и моментов пар
и моментов пар 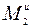 ,
,  через искомое ускорение
через искомое ускорение  , а также модуль силы трения скольжения
, а также модуль силы трения скольжения  :
:
 ;
;
 ;
; 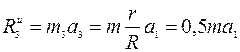 ;
;
 ;
; 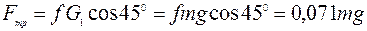
и подставим вычисленные величины в уравнение (5):
 .
.
Отсюда  м/с2;
м/с2;  м/с2.
м/с2.
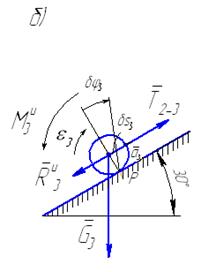
Для определения силы натяжения ветви 1−2 нити в качестве объекта исследования рассмотрим груз 1, заменяя действие нити на него соответствующей реакцией  (рис. 66, а).
(рис. 66, а).
Рис. 66
Общее уравнение динамики в этом случае имеет следующий
вид:


откуда

Для определения силы натяжения нити 2−3 рассмотрим каток 3 как объект исследования и заменим действие на него нити соответствующей реакцией 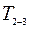 (рис. 66, б).
(рис. 66, б).
Общее уравнение динамики, составленное для катка 3, имеет вид:
 .
.
Отсюда

и 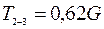 .
.
Ответ:  м/с2;
м/с2;  м/с2;
м/с2;  ;
; 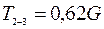 .
.
МЕТОД ОБОБЩЕННЫХ КООРДИНАТ
И УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
Не нашли, что искали? Воспользуйтесь поиском: