
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
К исследованию движения материальной точки
Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости (рис. 17−21). Найти скорость шарика  и
и  в положениях В и С и силу давления
в положениях В и С и силу давления  шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь
шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь  , отделяется от пружины.
, отделяется от пружины.
Необходимые для решения данные приведены в табл. 3.
В задании приняты следующие обозначения: т − масса шарика;  − начальная скорость шарика;
− начальная скорость шарика; 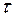 − время движения шарика на участке АВ (в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке ВD (в вариантах 3, 4, 6, 7,
− время движения шарика на участке АВ (в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке ВD (в вариантах 3, 4, 6, 7,
9−13, 15−17, 19, 22, 25, 26, 28, 29); 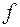 − коэффициент трения
− коэффициент трения
 Рис. 17
Рис. 17
 Рис. 18
Рис. 18
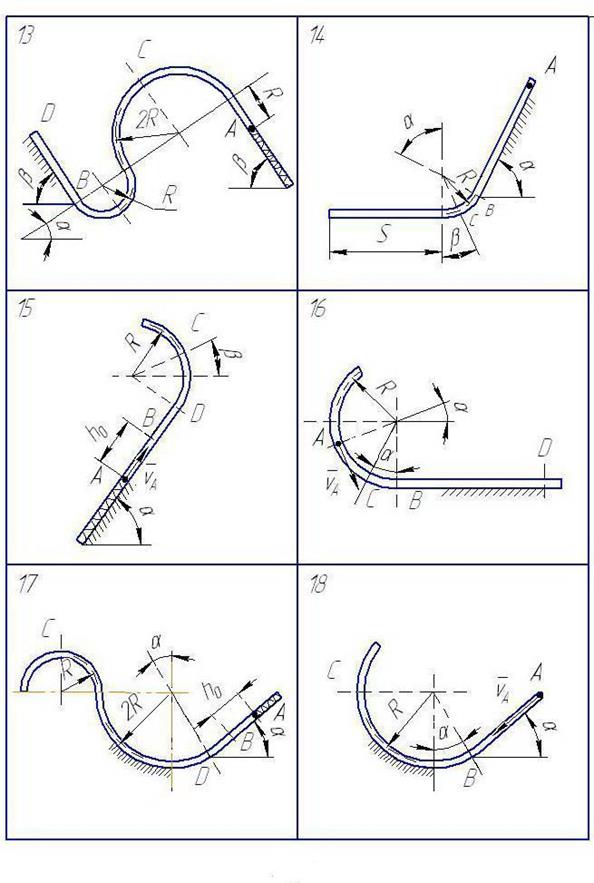
Рис. 19
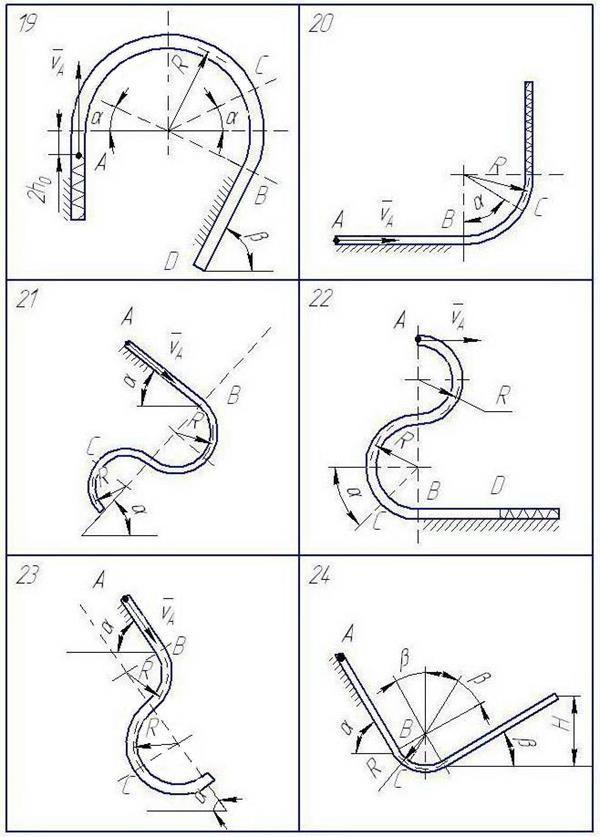
Рис. 20
 Рис. 21
Рис. 21
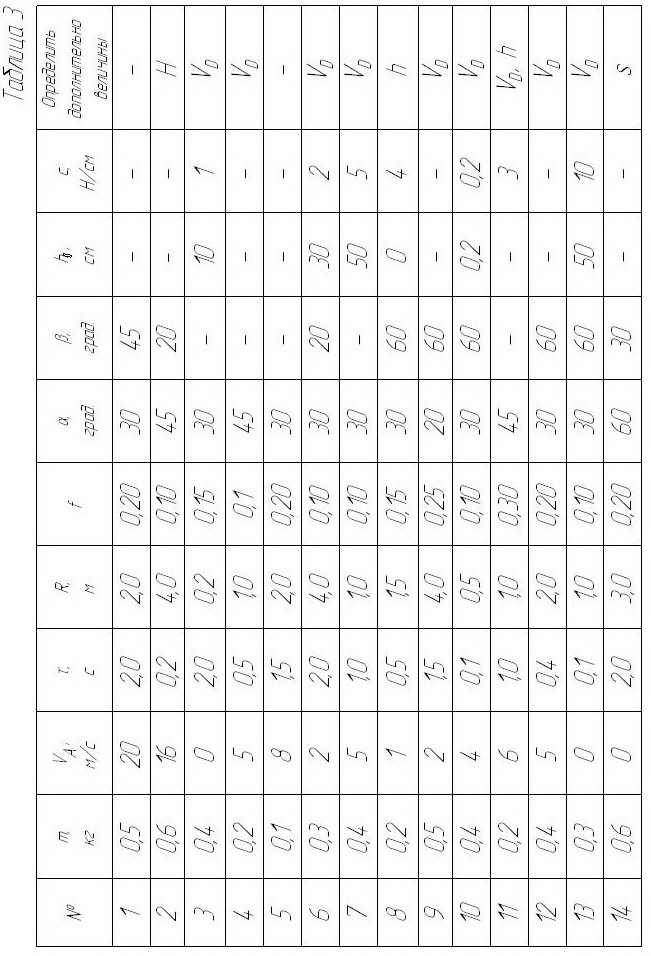
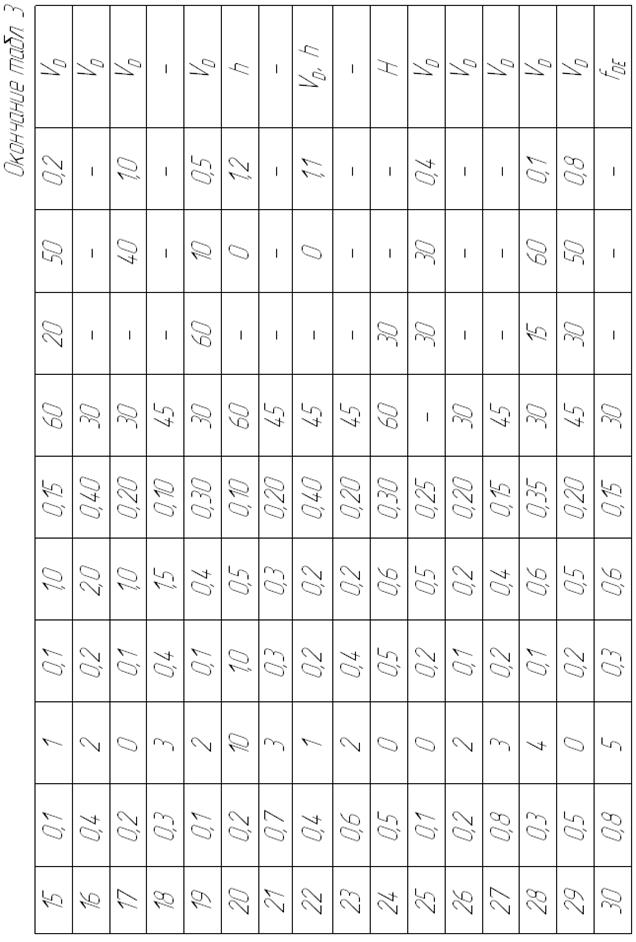
скольжения шарика по стенке трубки;  − начальная деформация пружины; h – наибольшее сжатие пружины; с − коэффициент жесткости пружины; Н − наибольшая высота подъема шарика; s − путь, пройденный шариком до остановки.
− начальная деформация пружины; h – наибольшее сжатие пружины; с − коэффициент жесткости пружины; Н − наибольшая высота подъема шарика; s − путь, пройденный шариком до остановки.
Пример выполнения задания (рис. 22). Дано: т = 0,5 кг,  м/с;
м/с; 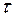 = 0,2 с (время движения на участке ВD); R =0,4 м;
= 0,2 с (время движения на участке ВD); R =0,4 м;  0,1;
0,1; 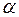 = 45°;
= 45°;  = 60°;
= 60°;  = 0; с = 20 Н/см = 2000 Н/м.
= 0; с = 20 Н/см = 2000 Н/м.
Определить  ,
,  ,
,  ,
,  ,
,  .
.
Решение. Для определения  и
и  применим теорему об изменении кинетической энергии материальной точки. Движение шарика на участках АС и АВ траектории происходит под действием силы тяжести
применим теорему об изменении кинетической энергии материальной точки. Движение шарика на участках АС и АВ траектории происходит под действием силы тяжести 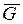 (силы трения на криволинейных участках не учитываем):
(силы трения на криволинейных участках не учитываем):
 °);
°); 
 ;
;
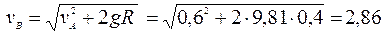 м/с;
м/с;
 °);
°);
 ;
;
 м/с.
м/с.
Определим силу давления шарика на стенку трубки в положении С. На шарик в этом случае действует сила тяжести 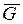 и сила реакции
и сила реакции  стенки трубки (рис. 22, б). Записав основное уравнение динамики материальной точки в проекциях на главную нормаль
стенки трубки (рис. 22, б). Записав основное уравнение динамики материальной точки в проекциях на главную нормаль 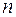 к траектории шарика в точке С, будем иметь:
к траектории шарика в точке С, будем иметь:
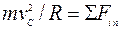 ;
;  .
.
Отсюда
 Н.
Н.
Искомая сила давления  шарика на стенку трубки по модулю равна найденной реакции
шарика на стенку трубки по модулю равна найденной реакции  и направлена в противоположную сторону (
и направлена в противоположную сторону ( .
.
Скорость шарика в положении D при его движении на участке BD траектории найдем с помощью теоремы об изменении количества
движения материальной точки, записав ее в проекциях на ось 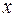
рис. 22, в):
 , (1)
, (1)
а)
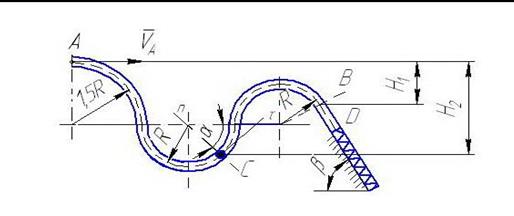
б) в)
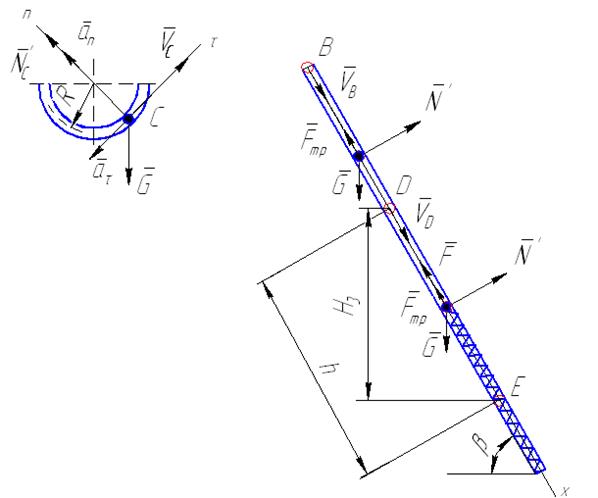
Рис. 22
где  − алгебраическая сумма проекций импульсов сил, приложен-
− алгебраическая сумма проекций импульсов сил, приложен-
ных к шарику за время его движения 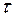 (с) на рассматриваемом участке траектории.
(с) на рассматриваемом участке траектории.
Так как к шарику приложены сила тяжести 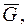 нормальная реакция
нормальная реакция  и сила трения
и сила трения  причем
причем
 ,
,
то
 .
.
Тогда из уравнения (1) получим
 ,
,
откуда
 м/с.
м/с.
Величину максимального сжатия  пружины определим из условия: в положении E при максимальном сжатии пружины скорость шарика равна нулю (
пружины определим из условия: в положении E при максимальном сжатии пружины скорость шарика равна нулю ( ). Тогда на основании теоремы об изменении кинетической энергии материальной точки на участке
). Тогда на основании теоремы об изменении кинетической энергии материальной точки на участке  движения шарика будем иметь:
движения шарика будем иметь:
 , (2)
, (2)
где
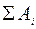 - алгебраическая сумма работ силы тяжести
- алгебраическая сумма работ силы тяжести 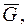 силы упруго-
силы упруго-
сти  нормальной реакции
нормальной реакции  и силы трения
и силы трения  , действующих на шарик на участке DE его траектории:
, действующих на шарик на участке DE его траектории:  . Учитывая, что
. Учитывая, что  , из уравнения (2) получим:
, из уравнения (2) получим:

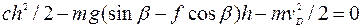
или
 . (3)
. (3)
Решая квадратное уравнение (2) относительно величины  , получим:
, получим:

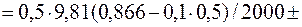
 м.
м.
Откуда, поскольку величина  положительна, искомая величина максимального сжатия пружины
положительна, искомая величина максимального сжатия пружины 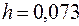 м.
м.
Ответ:  м/с;
м/с; 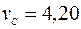 м/с;
м/с; 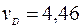 м/с;
м/с;  ;
;
 =0,073 м.
=0,073 м.
Не нашли, что искали? Воспользуйтесь поиском: