
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Критерий Коши и другие критерии сходимости для числовых рядов
Т.  , т.е любой отрезок ряда может быть сделан сколь угодно малым, начиная с некоторого номера.
, т.е любой отрезок ряда может быть сделан сколь угодно малым, начиная с некоторого номера.
Т. (критерий сх-ти ряда в терминах остатов)Сх-ть ряда ∑ak равносильна сх-ти любого его остатка. В случае сх-ти ряда посл-ть (rn) суммы остатков стремится к 0.
Т. (критерий сх-ти ряда с неотриц членами)Сх-ть числ ряда с неотриц членами равнос ограниченности сверху посл-ти его частных сумм.
66. Признаки сравнения для знакоположительных рядов.
Т. (Мажорантный признак сравнения). Пусть ∑ak и ∑bk ряды с неотриц членами и ak=O(bk) при k→∞, тогда: 1)Если ряд ∑bk сх-ся, то ряд ∑ak также сх-ся; 2) Если ряд ∑ak расх-ся, то ряд ∑bk также расх-ся.
Т. (признак сравнения в предельной форме).Пусть ∑bk и ∑ak-знакополож ряды и существует lim ak/bk=Lє[0;+∞), тогда: 1)При 0<L<+∞ ряды ∑bk и ∑ak оба сх-ся или расх; 2)При L=0 из сх ниж ряда из ∑bk вытекает сх-ть ряда ∑ak; 3)При L=+∞ из расход-ти верхнего ряда ∑ak вытекает расх-ть нижнего ряда ∑bk.
Т. (признак сравнения отношения).Пусть сумма ∑ak и ∑bk-знакоположит ряды и для всех вы прав-во: 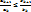 , тогда: 1)∑bk сх, тогда ∑ak сх; 2)∑ak расх, тогда ∑bk расх.
, тогда: 1)∑bk сх, тогда ∑ak сх; 2)∑ak расх, тогда ∑bk расх.
67. Интегральный признак сходимости для знакоположительных рядов. Следствия. Т. (Интеграл призн Маклорена-Коши).Пусть f:[1;+∞)→R-положит убывающ ф-ия, тогда сходимость числового ряда ∑f(x) равносильна существованию конечного lim f(x) первообразной F(x) для ф-ии f(x). Сл. Для гармонического ряда ∑  имеем f(x)=
имеем f(x)= 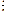 . Её первообразная F(x)=ln x→+∞, тогда ряд ∑
. Её первообразная F(x)=ln x→+∞, тогда ряд ∑  расх-ся.Из отношения Sn-f(1)
расх-ся.Из отношения Sn-f(1)  Sn-1 при f(x)=
Sn-1 при f(x)= 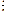 вытекает приближ знач для частных сумм гармонического ряда ∑
вытекает приближ знач для частных сумм гармонического ряда ∑  :
: 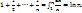 Более точная ф-ла:
Более точная ф-ла:  ,
,  →0, c=lim(
→0, c=lim(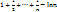 ) наз постоянной Эйлера(с=0,577…) 68. Признаки Коши и Даламбера
) наз постоянной Эйлера(с=0,577…) 68. Признаки Коши и Даламбера
Т. (Пр-к Коши(с корнем)). Пусть ∑ak-ряд с неотриц членами, для кот 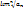 =q, тогда: 1)при q<1 ряд сх-ся; 2)при q>1 ряд расх-ся; 3)при q=1 необх дополн исслед ряда.
=q, тогда: 1)при q<1 ряд сх-ся; 2)при q>1 ряд расх-ся; 3)при q=1 необх дополн исслед ряда.
Т. (Пр-к Даламбера).Пусть для знакаположительного ряда ∑ak сущ-ет lim  =D, тогда: 1)при D<1 ряд сх-ся; 2)при D>1 ряд расх-ся; 3)при D=1 необх дополн исслед ряда.
=D, тогда: 1)при D<1 ряд сх-ся; 2)при D>1 ряд расх-ся; 3)при D=1 необх дополн исслед ряда.
Не нашли, что искали? Воспользуйтесь поиском: